Асимптотика гипергеометрических последовательностей — различия между версиями
Iksiygrik (обсуждение | вклад) м |
Iksiygrik (обсуждение | вклад) м |
||
| Строка 17: | Строка 17: | ||
Перепишем отношение <tex>\cfrac{a_{n+1}}{a_n}</tex> в виде | Перепишем отношение <tex>\cfrac{a_{n+1}}{a_n}</tex> в виде | ||
| − | <tex>\cfrac{a_{n+1}}{a_n}=A \cdot \cfrac{1 + \alpha_1 \cdot n^{-1} + \ldots + \alpha_k \cdot n^{-k}}{1 + \beta_1 \cdot n^{-1} + \ldots + \beta_k \cdot n^{-k}}=A \cdot f(\cfrac{1}{n})</tex>, | + | <tex>\cfrac{a_{n+1}}{a_n}=A \cdot \cfrac{1 + \alpha_1 \cdot n^{-1} + \ldots + \alpha_k \cdot n^{-k}}{1 + \beta_1 \cdot n^{-1} + \ldots + \beta_k \cdot n^{-k}}=A \cdot f\left(\cfrac{1}{n}\right)</tex>, |
где | где | ||
| Строка 25: | Строка 25: | ||
Прологарифмировав отношение <tex>\cfrac{a_{n+1}}{a_n}</tex>, получаем | Прологарифмировав отношение <tex>\cfrac{a_{n+1}}{a_n}</tex>, получаем | ||
| − | <tex>\ln a_{n+1} - \ln a_n = \ln A + \ln f(\cfrac{1}{n})</tex>. | + | <tex>\ln a_{n+1} - \ln a_n = \ln A + \ln f\left(\cfrac{1}{n}\right)</tex>. |
Посмотрим на функцию <tex>\ln f(x)</tex>. Выпишем начальные члены разложения функции <tex>f</tex> в ряд в точке <tex>0</tex>: | Посмотрим на функцию <tex>\ln f(x)</tex>. Выпишем начальные члены разложения функции <tex>f</tex> в ряд в точке <tex>0</tex>: | ||
| Строка 57: | Строка 57: | ||
<tex>+ | \ln a_{n+m} - \ln a_{n+m-1} - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n+m}| + | \alpha_1 - \beta_1 | \cdot | \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n | \leqslant</tex> | <tex>+ | \ln a_{n+m} - \ln a_{n+m-1} - \ln A - (\alpha_1 - \beta_1) \cdot \cfrac{1}{n+m}| + | \alpha_1 - \beta_1 | \cdot | \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n | \leqslant</tex> | ||
| − | <tex>\leqslant C \cdot (\cfrac{1}{n^2} + \cfrac{1}{(n+1)^2} + \ldots + \cfrac{1}{(n+m-1)^2}) + | \alpha_1 - \beta_1 | \cdot | \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n |</tex>. | + | <tex>\leqslant C \cdot \left(\cfrac{1}{n^2} + \cfrac{1}{(n+1)^2} + \ldots + \cfrac{1}{(n+m-1)^2}\right) + | \alpha_1 - \beta_1 | \cdot | \sum\limits_{k=0}^{m-1} \cfrac{1}{n+k} - \ln {(n+m)} + \ln n |</tex>. |
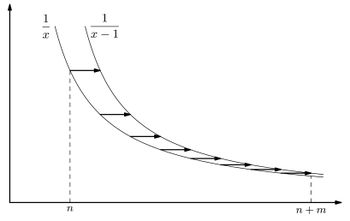
Поскольку ряд <tex>\sum\limits_{k=1}^{\infty} \cfrac{1}{k^2}</tex> сходится, первое слагаемое в правой части последнего неравенства при больших <tex>n</tex> можно сделать сколь угодно малым. Чтобы оценить второе слагаемое, заметим, что стоящая в нем сумма представляет собой площадь под графиком ступенчатой функции <tex>\cfrac{1}{[x]}</tex> на отрезке <tex>[n, n+m]</tex>, | Поскольку ряд <tex>\sum\limits_{k=1}^{\infty} \cfrac{1}{k^2}</tex> сходится, первое слагаемое в правой части последнего неравенства при больших <tex>n</tex> можно сделать сколь угодно малым. Чтобы оценить второе слагаемое, заметим, что стоящая в нем сумма представляет собой площадь под графиком ступенчатой функции <tex>\cfrac{1}{[x]}</tex> на отрезке <tex>[n, n+m]</tex>, | ||
| Строка 66: | Строка 66: | ||
(Здесь через <tex>[x]</tex> обозначена целая часть числа <tex>x</tex>, наибольшее целое число, не превосходящее <tex>x</tex>.) Эта площадь больше, чем площадь под графиком функции <tex>y = \cfrac{1}{x}</tex>, но меньше, чем площадь под графиком функции <tex>y = \cfrac{1}{x-1}</tex> на этом же отрезке. Площадь под графиком функции <tex>y = \cfrac{1}{x-1}</tex> равна <tex>\ln {(n+m-1)} - \ln {(n-1)}</tex>. Таким образом, интересующая нас разность не превосходит <tex>|(\ln {(n+m-1)} - \ln {(n-1)}) - (- \ln {(n+m)} + \ln n)| =</tex> | (Здесь через <tex>[x]</tex> обозначена целая часть числа <tex>x</tex>, наибольшее целое число, не превосходящее <tex>x</tex>.) Эта площадь больше, чем площадь под графиком функции <tex>y = \cfrac{1}{x}</tex>, но меньше, чем площадь под графиком функции <tex>y = \cfrac{1}{x-1}</tex> на этом же отрезке. Площадь под графиком функции <tex>y = \cfrac{1}{x-1}</tex> равна <tex>\ln {(n+m-1)} - \ln {(n-1)}</tex>. Таким образом, интересующая нас разность не превосходит <tex>|(\ln {(n+m-1)} - \ln {(n-1)}) - (- \ln {(n+m)} + \ln n)| =</tex> | ||
| − | <tex>= | \ln {(1 - \cfrac{1}{n+m})} - \ln {(1 - \cfrac{1}{n})}| <</tex> | + | <tex>= | \ln {\left(1 - \cfrac{1}{n+m}\right)} - \ln {\left(1 - \cfrac{1}{n}\right)}| <</tex> |
| − | <tex>< |\ln {(1 - \cfrac{1}{n})}| < C \cdot \cfrac{1}{n}</tex>. | + | <tex>< |\ln {\left(1 - \cfrac{1}{n}\right)}| < C \cdot \cfrac{1}{n}</tex>. |
}} | }} | ||
| Строка 82: | Строка 82: | ||
уже известна, например, при <tex>\alpha=−1</tex>. Согласно определению функции <tex>(1-s)^{\alpha}</tex> имеем | уже известна, например, при <tex>\alpha=−1</tex>. Согласно определению функции <tex>(1-s)^{\alpha}</tex> имеем | ||
| − | <tex>(a-s)^{\alpha}=a^{\alpha} \cdot (1-\cfrac{s}{a})^{\alpha}=a^{\alpha} \cdot (1 - \cfrac{\alpha}{1!} \cdot \cfrac{s}{a} + \cfrac{\alpha \cdot (\alpha-1)}{2!} \cdot {(\cfrac{s}{a})^2} - \cfrac{\alpha \cdot (\alpha-1) \cdot (\alpha-2)}{3!} \cdot (\cfrac{s}{a})^3 + \ldots)</tex> | + | <tex>(a-s)^{\alpha}=a^{\alpha} \cdot \left(1-\cfrac{s}{a}\right)^{\alpha}=a^{\alpha} \cdot \left(1 - \cfrac{\alpha}{1!} \cdot \cfrac{s}{a} + \cfrac{\alpha \cdot (\alpha-1)}{2!} \cdot {\left(\cfrac{s}{a}\right)^2} - \cfrac{\alpha \cdot (\alpha-1) \cdot (\alpha-2)}{3!} \cdot \left(\cfrac{s}{a}\right)^3 + \ldots \right)</tex> |
| − | Если <tex>\alpha</tex> — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае начиная с некоторого номера все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться леммой при <tex>a_n=(-1)^n \cdot \cfrac{\alpha \cdot (\alpha-1) \cdot \ldots \cdot (\alpha-n+1)}{n! \cdot {\alpha}^n}</tex> | + | Если <tex>\alpha</tex> — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае, начиная с некоторого номера, все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться леммой при <tex>a_n=(-1)^n \cdot \cfrac{\alpha \cdot (\alpha-1) \cdot \ldots \cdot (\alpha-n+1)}{n! \cdot {\alpha}^n}:</tex> |
<tex>\cfrac{a_{n+1}}{a_n}=\cfrac{1}{a} \cdot \cfrac{n-\alpha}{n+1}</tex> | <tex>\cfrac{a_{n+1}}{a_n}=\cfrac{1}{a} \cdot \cfrac{n-\alpha}{n+1}</tex> | ||
Версия 21:07, 8 июня 2018
| Определение: |
| Последовательность, в которой отношение двух соседних членов равно отношению многочленов степени , где , называется гипергеометрической (англ. hypergeometric sequence). |
Вычисление асимптотики
| Лемма: |
Пусть последовательность положительных чисел такова, что для всех достаточно больших , причем . Тогда растет как для некоторой постоянной . |
| Доказательство: |
|
Утверждение леммы эквивалентно тому, что существует предел . Для доказательства существования предела применим критерий Коши[1], т. е. будем доказывать, что рассматриваемая последовательность фундаментальна[2]. Перепишем отношение в виде , где
Прологарифмировав отношение , получаем . Посмотрим на функцию . Выпишем начальные члены разложения функции в ряд в точке : для некоторой константы . Это разложение - самый существенный элемент доказательства. Именно коэффициент (отличный от нуля по предположению леммы) при линейном члене указывает на присутствие сомножителя в асимптотике. Для логарифма функции имеем
Поэтому для некоторой постоянной при достаточно маленьком имеем . В частности, если достаточно велико, то , ,
. Теперь интересующее нас выражение в левой части неравенства можно оценить с помощью системы и неравенства треугольника[3]:
. Поскольку ряд сходится, первое слагаемое в правой части последнего неравенства при больших можно сделать сколь угодно малым. Чтобы оценить второе слагаемое, заметим, что стоящая в нем сумма представляет собой площадь под графиком ступенчатой функции на отрезке ,
. |
Замечание: Предположения леммы не позволяют определить величину константы . Действительно, умножив последовательность на произвольную постоянную , мы получим новую последовательность с тем же отношением последовательных членов, константа для которой увеличивается в раз
Примеры
Пример. Для чисел Каталана имеем
Поэтому для некоторой постоянной .
Пример. Найдем асимптотику коэффициентов для функции , где вещественно. В ряде случаев эта асимптотика нам уже известна, например, при . Согласно определению функции имеем
Если — целое неотрицательное число, то ряд обрывается и вопроса об асимптотике не возникает. В противном случае, начиная с некоторого номера, все коэффициенты ряда имеют одинаковый знак. Для определения асимптотики мы можем воспользоваться леммой при
Поэтому . Например, коэффициенты функции ведут себя как , и мы получаем повторный вывод ассимптотики для чисел Каталана.