Матроид Вамоса — различия между версиями
| Строка 50: | Строка 50: | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
==См. также== | ==См. также== | ||
| Строка 58: | Строка 55: | ||
* [[Примеры матроидов]] | * [[Примеры матроидов]] | ||
* [[Двойственный матроид]] | * [[Двойственный матроид]] | ||
| + | |||
| + | |||
| + | == Источники информации == | ||
| + | *[http://en.wikipedia.org/wiki/V%C3%A1mos_matroid Wikipedia {{---}} Vámos matroid] | ||
| + | *[http://www.lib.susu.ac.ru/ftd?base=SUSU_METHOD&key=000305409&dtype=F&etype=.pdf Элементарное введение в матроиды] | ||
| + | |||
[[Категория:Дискретная математика и алгоритмы]] | [[Категория:Дискретная математика и алгоритмы]] | ||
[[Категория:Матроиды]] | [[Категория:Матроиды]] | ||
[[Категория:Основные факты теории матроидов]] | [[Категория:Основные факты теории матроидов]] | ||
Версия 17:52, 17 октября 2018
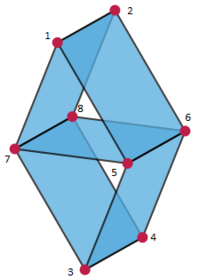
Матроид Вамоса или куб Вамоса — это матроид над восьмиэлементным множеством, который не изоморфен матричному ни над каким полем. Он назван в честь английского математика Питера Вамоса (Peter Vámos), который первым описал его в неопубликованной рукописи в 1968.
Содержание
Задание матроида
Пусть . Матроид Вамоса удобно задать, назвав все его зависимые множества: это все подмножества , в которых не менее пяти элементов, а также .
| Теорема: |
Заданная конструкция является матроидом. |
| Доказательство: |
| Выполнение первых двух аксиом очевидно. В проверке нуждается лишь тот факт, что если и независимые множества и , , то в найдется такой элемент , что — независимое множество. Когда , это очевидно. В противном же случае множество содержит по меньшей мере два различных элемента. Обозначим их через и . Теперь осталось заметить, что из множеств и хотя бы одно независимое, так как по условию нет двух зависимых множеств из четырех элементов, отличающихся одним элементом. |
Свойства
- Все циклы матроида Вамоса имеют размер по меньшей мере равный его рангу (максимальный размер независимого множества).
- Матроид Вамоса изоморфен своему двойственному матроиду. Однако он не самодвойственен, так как это требует нетривиальную перестановку элементов.
- Многочлен Татта матроида Вамоса равен
- Матроид Вамоса не является матричным.
Матроид Вамоса не представим ни над каким полем
| Теорема: |
Матроид Вамоса не представим ни над каким полем. |
| Доказательство: |
|
Это значит, что не существует векторного пространства и системы из восьми векторов в нем, таких что матроид линейной независимости этих векторов изоморфен матроиду Вамоса. Предположим, что существует изоморфный векторный матроид , где , и для каждого вектор соответствует элементу матроида Вамоса. Множество является базисом (так как — независимое множество в матроиде Вамоса). Запишем координаты каждого вектора в этом базисе: . Для дальнейшего нам понадобятся также векторы и , где . Ввиду линейной зависимости векторов (соответствуют зависимому множеству в матроиде Вамоса) получаем равенство нулю определителя, составленного из координат этих векторов:
отсюда
то есть векторы и линейно зависимы. Заметим, что вектор ненулевой (иначе были бы линейно зависимыми векторы , а у нас любые три вектора линейно независимые) . Поэтому для некоторого скаляра (то есть элемента числового поля, над которым рассматривается линейное пространство) имеет место равенство . Точно так же из линейной зависимости четвёрок векторов получаем соответственно равенства , где греческими буквами обозначены некоторые скаляры. Наконец, используем линейную зависимость векторов . С помощью найденных соотношений будем преобразовывать определитель, составленный из координат этих векторов (при этом вместо строк определителя для наглядности записываем поначалу соответствующие векторы):
Теперь заметим, что (в противном случае линейно зависимыми будут векторы и , а (иначе линейно зависимы векторы и ) . Поэтому равен нулю один из определителей или , например - первый из них. Но тогда то есть векторы линейно зависимы, что противоречит условию. |
См. также