Алгоритм масштабирования потока — различия между версиями
Bloof (обсуждение | вклад) |
Bloof (обсуждение | вклад) (→Псевдокод) |
||
| Строка 14: | Строка 14: | ||
<tex>\Delta\leftarrow 2^{\lfloor\log_2U\rfloor}</tex> | <tex>\Delta\leftarrow 2^{\lfloor\log_2U\rfloor}</tex> | ||
'''while''' <tex>\Delta>0</tex> | '''while''' <tex>\Delta>0</tex> | ||
| − | '''while''' в <tex>G_f</tex> существует <tex>s-t</tex> путь с пропускной способностью большей <tex>\Delta</tex> | + | '''do''' '''while''' в <tex>G_f</tex> существует <tex>s-t</tex> путь с пропускной способностью большей <tex>\Delta</tex> |
| − | + | '''do''' <tex>P\leftarrow</tex> путь с пропускной способностью большей <tex>\Delta</tex> | |
| − | + | <tex>\delta\leftarrow\min\{c_{ij}\colon(i,j)\in P\}</tex> | |
| − | + | увеличить поток по ребрам <tex>P</tex> на <tex>\delta</tex> | |
| − | + | обновить <tex>G_f</tex> | |
| − | + | <tex>f\leftarrow f+\delta</tex> | |
| − | + | <tex>\Delta\leftarrow\Delta/2</tex> | |
| − | |||
== Литература == | == Литература == | ||
* [http://www.csd.uwo.ca/~yuri/Papers/iccv07_cap_scaling.pdf ''Olivier Juan, Yuri Boikov'': Capacity Scaling for Graph Cuts in Vision] | * [http://www.csd.uwo.ca/~yuri/Papers/iccv07_cap_scaling.pdf ''Olivier Juan, Yuri Boikov'': Capacity Scaling for Graph Cuts in Vision] | ||
* [http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlowRevisited Algorithm Tutorials. Maximum Flow: Augmenting Path Algorithms Comparison] | * [http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlowRevisited Algorithm Tutorials. Maximum Flow: Augmenting Path Algorithms Comparison] | ||
Версия 21:26, 15 января 2011
Алгоритм масштабирования потока - алгоритм поиска максимального потока путем регулирования пропускной способности ребер. Этот алгоритм работает в предположении, что все пропускные способности ребер целые.
Содержание
Суть
Пусть есть граф , . Суть алгоритма в нахождении сначала путей с высокой пропускной способностью, чтобы сразу сильно увеличивать поток. Пусть - максимальная пропускная способность. Введем параметр . На каждом шаге будем искать в остаточном графе увеличивающие пути с пропускной способностью не меньше и увеличивать поток вдоль этих путей. В конце шага будем уменьшать в два раза, и на следующем шаге будем искать увеличивающий путь с новым . При алгоритм масштабирования идентичен алгоритму Эдмондса - Карпа, поэтому алгоритм масштабирования корректен.
Оценка сложности
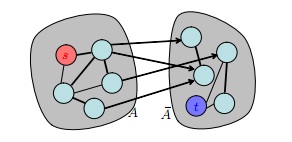
На каждом шаге алгоритм выполняет увеличений потока в худшем случае. Докажем это. . В конце шага множество вершин множество вершин можно разбить на две части: и . Все ребра выходящие из имеют остаточную пропускную способность менее . Наибольшее количество ребер между и равно . Итого остаточный поток(поток, который может быть получен на оставшихся шагах) на текущей фазе с максимально составляет . Каждый увеличивающий путь при данном имеет пропускную способность как минимум . На предыдущем шаге с масштабом остаточный поток ограничен . Значит максимальное число появившихся увеличивающих путей равно . Увеличивающий путь можно найти за , используя BFS. Количество шагов . Итоговая сложность .
Псевдокод
Capacity-Scaling
while
do while в существует путь с пропускной способностью большей
do путь с пропускной способностью большей
увеличить поток по ребрам на
обновить