Детерминированные автоматы с магазинной памятью — различия между версиями
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | Определим <tex>P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)</tex> как <b> | + | Определим <tex>P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)</tex> как <b>автомат с магазинной (стековой) памятью</b>, где <br> |
* <tex>Q</tex>: конечное множество состояний. | * <tex>Q</tex>: конечное множество состояний. | ||
* <tex>\Sigma</tex>: конечное множество входных символов. | * <tex>\Sigma</tex>: конечное множество входных символов. | ||
* <tex>\Gamma</tex>: конечный магазинный алфавит {{---}} множество символов, которые можно помещать в магазин. | * <tex>\Gamma</tex>: конечный магазинный алфавит {{---}} множество символов, которые можно помещать в магазин. | ||
| − | * <tex>\delta</tex>: функция переходов. <tex>\delta (q,a,X)=(p,\gamma)</tex> | + | * <tex>\delta</tex>: функция переходов. <tex>\delta (q,a,X)=(p,\gamma)</tex>, где |
** <tex>q</tex>: текущее состояние из Q. | ** <tex>q</tex>: текущее состояние из Q. | ||
| − | ** <tex>a</tex>: входной символ. | + | ** <tex>a</tex>: входной символ или <tex>\epsilon</tex>. |
** <tex>X</tex>: магазинный символ из <tex>\Gamma</tex>. | ** <tex>X</tex>: магазинный символ из <tex>\Gamma</tex>. | ||
** <tex>p</tex>: новое состояние из Q. | ** <tex>p</tex>: новое состояние из Q. | ||
| Строка 15: | Строка 15: | ||
* <tex>F</tex>: множество допускающих состояний. | * <tex>F</tex>: множество допускающих состояний. | ||
}} | }} | ||
| − | + | {{Определение | |
| + | |definition = | ||
| + | Определим <b>детерминированный автомат с магазинной (стековой) памятью</b> как автомат с магазинной памятью, в котором <br> | ||
| + | #<tex>\delta (q,a,X)</tex> имеет не более одного элемента для каждого <tex>q \in Q, a \in \Sigma</tex> или <tex>a=\epsilon, X \in \Gamma</tex>. | ||
| + | #Если <tex>\delta (q,a,X)</tex> непусто для некоторого <tex>a \in \Sigma</tex>, то <tex>\delta (q,\epsilon,X)</tex> должно быть пустым. | ||
| + | }} | ||
Будем обозначать переход автомата из состояния <tex>(q_1,a_1,X_1)</tex> в состояние <tex>(q_2,a_2,X_2)</tex> как <tex>(q_1,a_1,X_1)\vdash(q_2,a_2,X_2)</tex>. Переход автомата из состояния <tex>(q_1,a_1,X_1)</tex> в состояние <tex>(q_{p+1},a_{p+1},X_{p+1})</tex> через <tex>P</tex> промежуточных состояний обозначаем <tex>(q_1,a_1,X_1)\vdash^*_P(q_{p+1},a_{p+1},X_{p+1})</tex>. | Будем обозначать переход автомата из состояния <tex>(q_1,a_1,X_1)</tex> в состояние <tex>(q_2,a_2,X_2)</tex> как <tex>(q_1,a_1,X_1)\vdash(q_2,a_2,X_2)</tex>. Переход автомата из состояния <tex>(q_1,a_1,X_1)</tex> в состояние <tex>(q_{p+1},a_{p+1},X_{p+1})</tex> через <tex>P</tex> промежуточных состояний обозначаем <tex>(q_1,a_1,X_1)\vdash^*_P(q_{p+1},a_{p+1},X_{p+1})</tex>. | ||
Версия 21:32, 23 января 2011
| Определение: |
Определим как автомат с магазинной (стековой) памятью, где
|
| Определение: |
Определим детерминированный автомат с магазинной (стековой) памятью как автомат с магазинной памятью, в котором
|
Будем обозначать переход автомата из состояния в состояние как . Переход автомата из состояния в состояние через промежуточных состояний обозначаем .
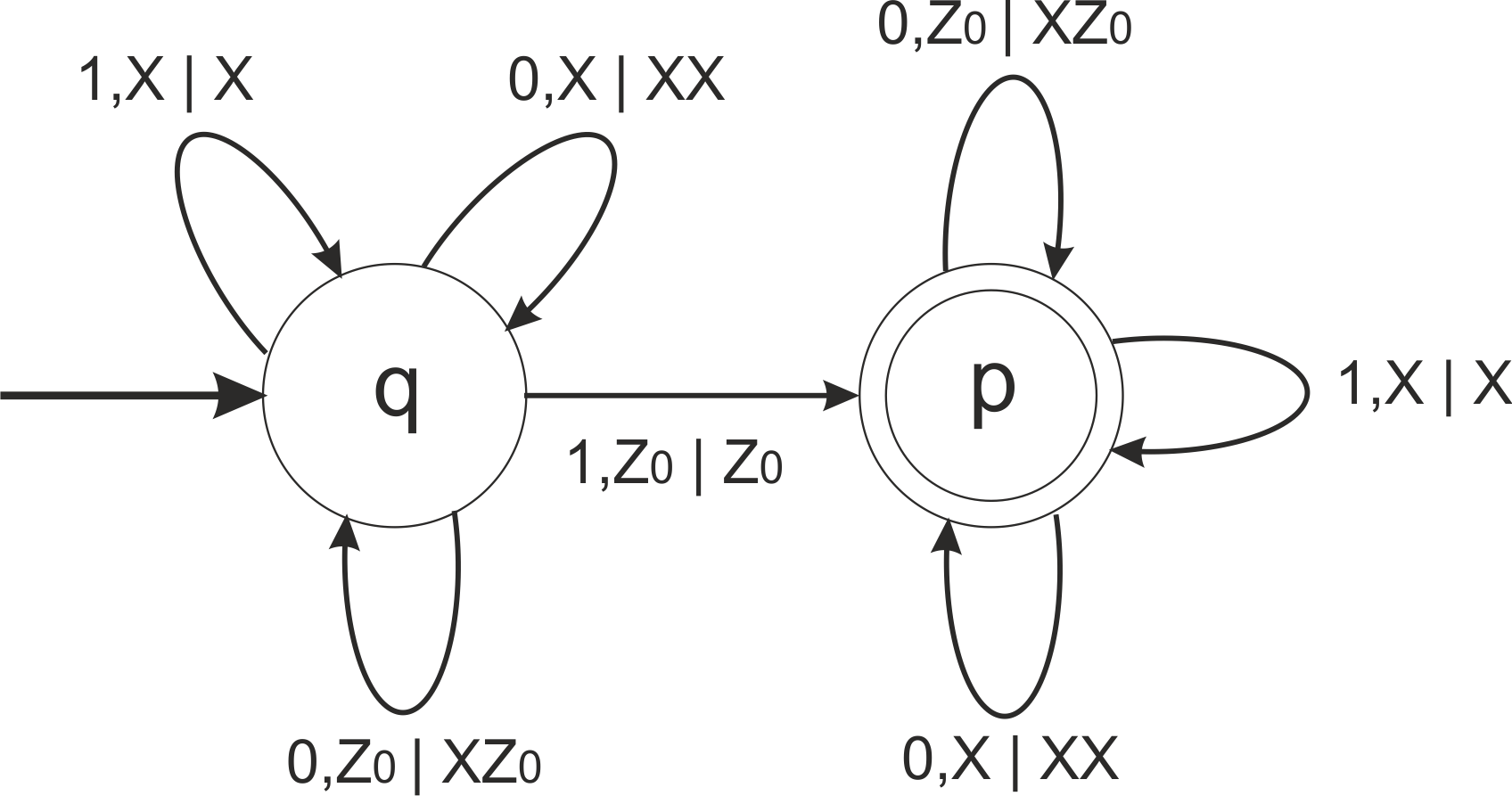
Пример
Автомат с функией перехода :