Level Ancestor problem — различия между версиями
| Строка 23: | Строка 23: | ||
Разобьем все вершины на пути следующим образом. Обойдем дерево с помощью обхода в глубину, пусть мы стоим в вершине | Разобьем все вершины на пути следующим образом. Обойдем дерево с помощью обхода в глубину, пусть мы стоим в вершине | ||
<tex>v</tex>, обойдем всех ее детей, добавив <tex>v</tex> в путь, идущий в самое глубокое поддерево, | <tex>v</tex>, обойдем всех ее детей, добавив <tex>v</tex> в путь, идущий в самое глубокое поддерево, | ||
| − | т.е. в котором находится вершина с | + | т.е. в котором находится вершина с самой большой глубиной. |
Для каждой вершины сохраним номер пути в который она входит. | Для каждой вершины сохраним номер пути в который она входит. | ||
=== Ladder decomposition === | === Ladder decomposition === | ||
| − | Увеличим каждый путь в два раза вверх, для каждого | + | Увеличим каждый путь в два раза вверх, для каждого нового пути сохраним все входящие в него вершины, |
а для каждой вершины сохраним ее номер в пути, в который она входит. Построение обычной longest-path декомпозиции займет у | а для каждой вершины сохраним ее номер в пути, в который она входит. Построение обычной longest-path декомпозиции займет у | ||
нас O(n) времени (обход в глубину), соответственно удлиннение каждого пути ухудшит ассимптотику до <tex>O(n \log n)</tex>. | нас O(n) времени (обход в глубину), соответственно удлиннение каждого пути ухудшит ассимптотику до <tex>O(n \log n)</tex>. | ||
| − | После этого посчитаем двоичные | + | === Двоичные подъемы === |
| + | После этого посчитаем двоичные подъемы для каждой вершины за <tex>O(\log n)</tex>, что соответственно не ухудшит ассимптотику. | ||
Пусть после этого нам пришел запрос <tex>LA(v, k)</tex>. | Пусть после этого нам пришел запрос <tex>LA(v, k)</tex>. | ||
| + | |||
| + | *Сделаем один максимально большой прыжок вверх с помощью насчитанных двоичных подъемов. | ||
| + | #<tex>i = \log k</tex> | ||
| + | #<tex>v = p_i[v]</tex> | ||
| + | * Рассмотрим путь, на котором лежит вершина <tex>v</tex> до удвоения. Он длины хотя бы <tex>2^i</tex>, так как мы точно знаем, что существует вершина потомок <tex>v</tex>, расстояние до которого ровно <tex>2^i</tex> (это вершина, из которой мы только что пришли). Значит, после удвоения этот путь стал длины хотя бы <tex>2^{i + 1}</tex>, причем хотя бы <tex>2^i</tex> вершин в нем - предки <tex>v</tex>. Это означает, что вершина, которую мы ищем, находится на этом пути (иначе бы мы могли до этого прыгнуть еще на <tex>2^i</tex> вверх). Так как мы знаем позицию <tex>v</tex> в этом пути, то нужную вершину мы можем найти за <tex>O(1)</tex>. | ||
| + | |||
| + | Таким образом, наш алгоритм работает за < <tex>O(n\log n), O(1)</tex> >. С помощью метода четырех русских данный метод можно улучшить до < <tex>O(n), O(1)</tex> > с помощью оптимизации предподсчета. | ||
Версия 23:54, 11 мая 2019
Задача о уровне предка (англ. "Level Ancestor problem") является задачей о превращении данного корневого дерева T в структуру данных, которая сможет определить предка любого узла на заданном расстоянии от корня дерева.
| Задача: |
| Дано корневое дерево c вершинами. Поступают запросы вида , для каждого из которых необходимо найти предка вершины , который находится на расстоянии от корня дерева . |
Содержание
Наивная реализация и двоичные подъемы
Используя обход в глубину посчитаем глубину каждой вершины дерева (это можно сделать за ), после чего можем из вершины подняться до необходимой глубины вершины , что так же в худшем случае работает за . Получили алгоритм за < >, где время ответа на запрос можно улучшить до c помощью предподсчета двоичных подъемов , но тогда и время предподсчета в наивной реализации (посчитать подъемы для всех вершин) ухудшится до < >. Альтернативой данным двум алгоритмам является полный предподсчет всех возможных запросов, что соответственно дает нам ассимптотику < >.
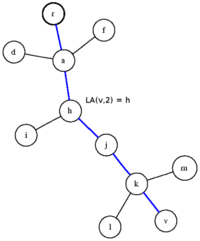
В данном примере поступает запрос , на который алгоритм должен дать ответ h.
Использование Heavy-light декомпозиции
Этот алгоритм базируется на различных способах декомпозиции дерева (выберем heavy-light декомпозицию), из свойств этого разбиения следует, что подняться на любую высоту из вершины мы можем за . Данное разбиение можно строить за , что дает нам алгоритм за < >.
Алгоритм лестниц
Longest path decomposition
Разобьем все вершины на пути следующим образом. Обойдем дерево с помощью обхода в глубину, пусть мы стоим в вершине , обойдем всех ее детей, добавив в путь, идущий в самое глубокое поддерево, т.е. в котором находится вершина с самой большой глубиной. Для каждой вершины сохраним номер пути в который она входит.
Ladder decomposition
Увеличим каждый путь в два раза вверх, для каждого нового пути сохраним все входящие в него вершины, а для каждой вершины сохраним ее номер в пути, в который она входит. Построение обычной longest-path декомпозиции займет у нас O(n) времени (обход в глубину), соответственно удлиннение каждого пути ухудшит ассимптотику до .
Двоичные подъемы
После этого посчитаем двоичные подъемы для каждой вершины за , что соответственно не ухудшит ассимптотику.
Пусть после этого нам пришел запрос .
- Сделаем один максимально большой прыжок вверх с помощью насчитанных двоичных подъемов.
- Рассмотрим путь, на котором лежит вершина до удвоения. Он длины хотя бы , так как мы точно знаем, что существует вершина потомок , расстояние до которого ровно (это вершина, из которой мы только что пришли). Значит, после удвоения этот путь стал длины хотя бы , причем хотя бы вершин в нем - предки . Это означает, что вершина, которую мы ищем, находится на этом пути (иначе бы мы могли до этого прыгнуть еще на вверх). Так как мы знаем позицию в этом пути, то нужную вершину мы можем найти за .
Таким образом, наш алгоритм работает за < >. С помощью метода четырех русских данный метод можно улучшить до < > с помощью оптимизации предподсчета.