Level Ancestor problem — различия между версиями
| Строка 55: | Строка 55: | ||
== Источники информации == | == Источники информации == | ||
| + | *https://www.cadmo.ethz.ch/education/lectures/HS18/SAADS/reports/5.pdf | ||
*https://en.wikipedia.org/wiki/Level_ancestor_problem | *https://en.wikipedia.org/wiki/Level_ancestor_problem | ||
Версия 13:21, 12 мая 2019
Задача о уровне предка (англ. "Level Ancestor problem") является задачей о превращении данного корневого дерева T в структуру данных, которая сможет определить предка любого узла на заданном расстоянии от корня дерева.
| Задача: |
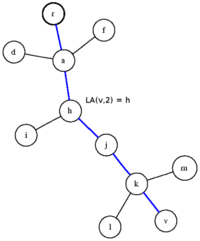
| Дано корневое дерево c вершинами. Поступают запросы вида , для каждого из которых необходимо найти предка вершины , который находится на расстоянии от корня дерева . |
Содержание
Наивная реализация и двоичные подъемы
Используя обход в глубину посчитаем глубину каждой вершины дерева (это можно сделать за ), после чего можем из вершины подняться до необходимой глубины вершины , что так же в худшем случае работает за . Получили алгоритм за < >, где время ответа на запрос можно улучшить до c помощью предподсчета двоичных подъемов , но тогда и время предподсчета в наивной реализации (посчитать подъемы для всех вершин) ухудшится до < >. Альтернативой данным двум алгоритмам является полный предподсчет всех возможных запросов, что соответственно дает нам ассимптотику < >.
В данном примере поступает запрос , на который алгоритм должен дать ответ h.
Использование Heavy-light декомпозиции
Этот алгоритм базируется на различных способах декомпозиции дерева (выберем heavy-light декомпозицию), из свойств этого разбиения следует, что подняться на любую высоту из вершины мы можем за . Данное разбиение можно строить за , что дает нам алгоритм за < >.
Алгоритм лестниц
Longest path decomposition
Разобьем все вершины на пути следующим образом. Обойдем дерево с помощью обхода в глубину, пусть мы стоим в вершине , обойдем всех ее детей, добавив в путь, идущий в самое глубокое поддерево, т.е. в котором находится вершина с самой большой глубиной. Для каждой вершины сохраним номер пути в который она входит.
Ladder decomposition
Увеличим каждый путь в два раза вверх, для каждого нового пути сохраним все входящие в него вершины, а для каждой вершины сохраним ее номер в пути, в который она входит. Построение обычной longest-path декомпозиции займет у нас времени (обход в глубину), соответственно удлиннение каждого пути ухудшит ассимптотику до .
Двоичные подъемы
После этого посчитаем двоичные подъемы для каждой вершины за , что соответственно не ухудшит ассимптотику.
Пусть после этого нам пришел запрос .
- Сделаем один максимально большой прыжок вверх с помощью насчитанных двоичных подъемов.
- Рассмотрим путь, на котором лежит вершина до удвоения. Он длины хотя бы , так как мы точно знаем, что существует вершина потомок , расстояние до которого ровно (это вершина, из которой мы только что пришли). Значит, после удвоения этот путь стал длины хотя бы , причем хотя бы вершин в нем - предки . Это означает, что вершина, которую мы ищем, находится на этом пути (иначе бы мы могли до этого прыгнуть еще на вверх). Так как мы знаем позицию в этом пути, то нужную вершину мы можем найти за .
Таким образом, наш алгоритм работает за < >. Методом четырех русских данный метод можно улучшить до < > с помощью оптимизации предподсчета.
The Macro-Micro-Tree Algorithm
В данном разделе мы докажем, что предподсчет предыдущего алгоритма можно улучшить до . Для начала рассмотрим алгоритм за < >, где это количество листьев.
- С помощью обхода в глубину запомним по одному листу в ее поддереве для каждой вершины
- Воспользуемся алгоритмом лестниц, но будем выполнять предподсчет только для листьев.
Рассмотрим как можно улучшить данный алгоритм:
- Зададим некую функцию
- Посчитаем размер поддерева для каждой вершины с помощью обхода в глубину, после чего удалим все вершины размер поддерева которых меньше чем .
- Забудем на время про удаленные поддеревья, для оставшегося дерева наш алгоритм даст < >. Что дает нам алгоритм за
< >. Для удаленных поддеревьев же выполним полный предподсчет: таких деревьев не более чем , что дает ассимптотику предподсчета .
В итоге полученный алгоритм действительно работает за <>.