CAP теорема — различия между версиями
Yeputons (обсуждение | вклад) |
Yeputons (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
Оригинальная формулировка — Brewer's Conjecture (2000), а формализовано в работе Gilbert & Lynch (2004). | Оригинальная формулировка — Brewer's Conjecture (2000), а формализовано в работе Gilbert & Lynch (2004). | ||
Там есть много тонкостей с тем, что такое "не отказавший узел", "одинаковые данные", "разрыв связи", "система продолжает работать", "когда система всё-таки окончательно ломается и считается недоступной" и тому подобное. | Там есть много тонкостей с тем, что такое "не отказавший узел", "одинаковые данные", "разрыв связи", "система продолжает работать", "когда система всё-таки окончательно ломается и считается недоступной" и тому подобное. | ||
| + | |||
| + | Для общей эрудиции выглядят неплохо статьи<ref>http://blog.thislongrun.com/2015/04/the-unclear-cp-vs-ca-case-in-cap.html</ref><ref>https://habr.com/ru/post/322276/</ref> | ||
== Классификация алгоритмов == | == Классификация алгоритмов == | ||
[[Файл:Distributed-cap.png|400px]] | [[Файл:Distributed-cap.png|400px]] | ||
Версия 21:04, 3 июня 2019
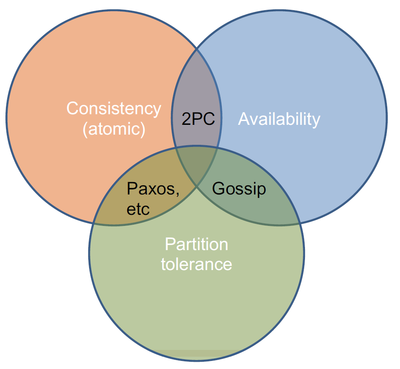
CAP-теорема — утверждение о том, что в распределённых системах нельзя одновременно добиться трёх свойств:
- Consistency — на всех не отказавших узлах одинаковые (с точки зрения пользователя) данные
- Availability — запросы ко всем не отказавшим узлам возвращают ответ
- Partition tolerance — даже если связь в системе стала несвязной, то система продолжает работать
Формально мы это не формулировали и не доказывали. Оригинальная формулировка — Brewer's Conjecture (2000), а формализовано в работе Gilbert & Lynch (2004). Там есть много тонкостей с тем, что такое "не отказавший узел", "одинаковые данные", "разрыв связи", "система продолжает работать", "когда система всё-таки окончательно ломается и считается недоступной" и тому подобное.
Для общей эрудиции выглядят неплохо статьи[1][2]
Классификация алгоритмов