Практики реализации нейронных сетей — различия между версиями
Sketcher (обсуждение | вклад) |
Sketcher (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | == Аугментация данных == | + | ==Аугментация данных== |
| − | == Дропаут == | + | ==Дропаут== |
| − | == Функции активации == | + | ==Функции активации== |
Одним из важнейших аспектов глубокой нейронной сети являются функции активации. | Одним из важнейших аспектов глубокой нейронной сети являются функции активации. | ||
{{Определение | {{Определение | ||
| − | |definition= '''Функция активации''' (англ. ''activation function'') определяет выходной сигнал нейрона в зависимости от | + | |definition= '''Функция активации''' (англ. ''activation function'') определяет выходной сигнал нейрона в зависимости от результата взвешенной суммы входов и порогового значения.}} |
Рассмотрим нейрон Z с выходным значением <math>Z = \sum\limits_{i} w_{i}x_{i} + bias</math>, где <tex>w_{i}</tex> и <tex>x_{i}</tex> {{---}} вес и входное значение <tex>i</tex>-ого входа, а <tex>bias</tex> {{---}} смещение. Полученный результат передается в функцию активации, которая решает рассматривать этот нейрон как активированный, или его можно игнорировать. | Рассмотрим нейрон Z с выходным значением <math>Z = \sum\limits_{i} w_{i}x_{i} + bias</math>, где <tex>w_{i}</tex> и <tex>x_{i}</tex> {{---}} вес и входное значение <tex>i</tex>-ого входа, а <tex>bias</tex> {{---}} смещение. Полученный результат передается в функцию активации, которая решает рассматривать этот нейрон как активированный, или его можно игнорировать. | ||
| − | |||
| − | === | + | ===Ступенчатая функция=== |
| − | === | + | ===Линейная функция=== |
| − | === | + | ===Сигмоида=== |
У ступенчатых функций есть определенное количество ограничений, связанных с ее линейностью. Если функция активации является линейной, то независимо от количества складываемых скрытых слоев в нейронной сети, конечный результат по-прежнему будет являться линейной комбинацией исходных входных данных. Эта линейность означает, что она не может реально охватить сложность нелинейных задач, таких как оператор XOR или различные паттерны, разделенные кривыми или кругами. Другой проблемой является то, что перцептрон со ступенчатой функцией не очень «стабилен», то есть может перейти из состояния 0 в 1 и из 0 в 1 при небольших изменениях в любом из весов входного слоя. | У ступенчатых функций есть определенное количество ограничений, связанных с ее линейностью. Если функция активации является линейной, то независимо от количества складываемых скрытых слоев в нейронной сети, конечный результат по-прежнему будет являться линейной комбинацией исходных входных данных. Эта линейность означает, что она не может реально охватить сложность нелинейных задач, таких как оператор XOR или различные паттерны, разделенные кривыми или кругами. Другой проблемой является то, что перцептрон со ступенчатой функцией не очень «стабилен», то есть может перейти из состояния 0 в 1 и из 0 в 1 при небольших изменениях в любом из весов входного слоя. | ||
| Строка 21: | Строка 20: | ||
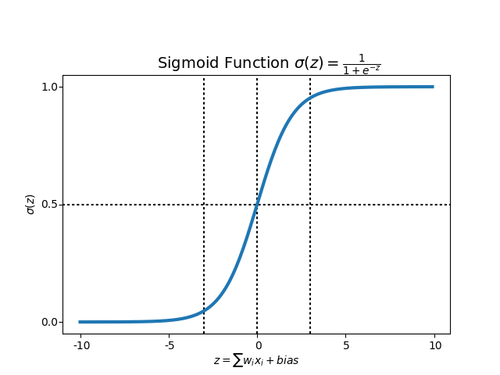
Sigmoid функция, в отличие от ступенчатой функции, вводит нелинейность в выбранную модель нейронной сети. Нелинейность означает, что выход, получаемый из нейрона произведением некоторых входов <math>x (x_1, x_2, ..., x_m)</math> и весов <math>w (w_1, w_2, ..., w_m)</math> плюс смещение, преобразованный сигмоидной функцией, не может быть представлен линейной комбинацией его входных сигналов. | Sigmoid функция, в отличие от ступенчатой функции, вводит нелинейность в выбранную модель нейронной сети. Нелинейность означает, что выход, получаемый из нейрона произведением некоторых входов <math>x (x_1, x_2, ..., x_m)</math> и весов <math>w (w_1, w_2, ..., w_m)</math> плюс смещение, преобразованный сигмоидной функцией, не может быть представлен линейной комбинацией его входных сигналов. | ||
| − | === | + | ===ReLU=== |
Несмотря на множество сильных сторон sigmoid функции, у нее есть значительные недостатки. Производная такой функции крайне мала во всех точках, кроме сравнительно небольшого промежутка. Это сильно усложняет процесс улучшения весов с помощью градиентного спуска. Эта проблема усугубляется в случае, если модель содержит больше слоев. Данная проблема называется проблемой исчезающего градиента.<ref>[https://en.wikipedia.org/wiki/Vanishing_gradient_problem Vanishing gradient problem, Wikipedia]</ref> | Несмотря на множество сильных сторон sigmoid функции, у нее есть значительные недостатки. Производная такой функции крайне мала во всех точках, кроме сравнительно небольшого промежутка. Это сильно усложняет процесс улучшения весов с помощью градиентного спуска. Эта проблема усугубляется в случае, если модель содержит больше слоев. Данная проблема называется проблемой исчезающего градиента.<ref>[https://en.wikipedia.org/wiki/Vanishing_gradient_problem Vanishing gradient problem, Wikipedia]</ref> | ||
| Строка 32: | Строка 31: | ||
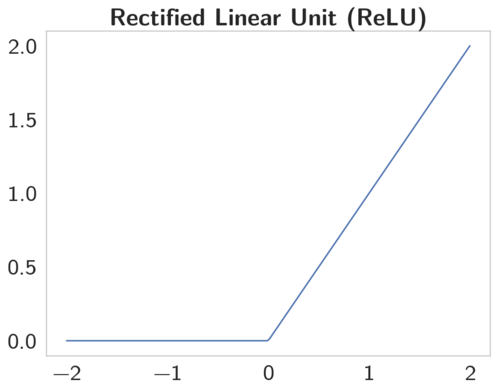
Функция ReLU отлично работает в большинстве приложений, в результате чего она получила широкое распространение. Данная функция позволяет правильно учитывать нелинейности и взаимодействия. | Функция ReLU отлично работает в большинстве приложений, в результате чего она получила широкое распространение. Данная функция позволяет правильно учитывать нелинейности и взаимодействия. | ||
| − | === | + | ===Функция гиперболического тангенса=== |
| − | == См. также== | + | ==См. также== |
| − | == Примечания == | + | ==Примечания== |
<references /> | <references /> | ||
| − | == Источники информации == | + | ==Источники информации== |
Версия 23:50, 25 февраля 2020
Содержание
Аугментация данных
Дропаут
Функции активации
Одним из важнейших аспектов глубокой нейронной сети являются функции активации.
| Определение: |
| Функция активации (англ. activation function) определяет выходной сигнал нейрона в зависимости от результата взвешенной суммы входов и порогового значения. |
Рассмотрим нейрон Z с выходным значением , где и — вес и входное значение -ого входа, а — смещение. Полученный результат передается в функцию активации, которая решает рассматривать этот нейрон как активированный, или его можно игнорировать.
Ступенчатая функция
Линейная функция
Сигмоида
У ступенчатых функций есть определенное количество ограничений, связанных с ее линейностью. Если функция активации является линейной, то независимо от количества складываемых скрытых слоев в нейронной сети, конечный результат по-прежнему будет являться линейной комбинацией исходных входных данных. Эта линейность означает, что она не может реально охватить сложность нелинейных задач, таких как оператор XOR или различные паттерны, разделенные кривыми или кругами. Другой проблемой является то, что перцептрон со ступенчатой функцией не очень «стабилен», то есть может перейти из состояния 0 в 1 и из 0 в 1 при небольших изменениях в любом из весов входного слоя.
Для того, чтобы избежать данных проблем, в нейронных сетях используется сигмоидная функция в качестве активационной. Также ее еще называют логистической.
Sigmoid функция, в отличие от ступенчатой функции, вводит нелинейность в выбранную модель нейронной сети. Нелинейность означает, что выход, получаемый из нейрона произведением некоторых входов и весов плюс смещение, преобразованный сигмоидной функцией, не может быть представлен линейной комбинацией его входных сигналов.
ReLU
Несмотря на множество сильных сторон sigmoid функции, у нее есть значительные недостатки. Производная такой функции крайне мала во всех точках, кроме сравнительно небольшого промежутка. Это сильно усложняет процесс улучшения весов с помощью градиентного спуска. Эта проблема усугубляется в случае, если модель содержит больше слоев. Данная проблема называется проблемой исчезающего градиента.[1]
Функция ReLU имеет производную равную 0 для всех отрицательных значениях и 1 для положительных. Таким образом, когда обучение происходит на датасетах разумного размера, обычно находятся точки данных, дающие положительные значения для любого выбранного узла. Таким образом, средняя производная редко бывает близка к 0, что позволяет продолжать градиентный спуск.
Rectified Linear Unit — это наиболее часто используемая активационная функция при глубоком обучении. Данная функция возвращает 0, если принимает отрицательный вход, в случае же положительного входа, функция возвращает само число. Таким образом функция может быть записана как .
Функция ReLU отлично работает в большинстве приложений, в результате чего она получила широкое распространение. Данная функция позволяет правильно учитывать нелинейности и взаимодействия.