Обучение в реальном времени — различия между версиями
(→Математическая основа) |
|||
| Строка 21: | Строка 21: | ||
=== Функция ожидаемого риска (Expected Risk Function) === | === Функция ожидаемого риска (Expected Risk Function) === | ||
| + | Цель системы обучения состоит в поиске минимум функции <tex>J(w)</tex>, называемой функцией ожидаемого риска. | ||
| + | Эта функция раскладывается следующим образом: | ||
| + | <tex>J(w) \stackrel{\triangle}{=} E_z\ Q(z,w) \stackrel{\triangle}{=} \int Q(z,w)\,\mathrm{d}P(z) </tex> | ||
| − | <tex> | + | Переменная минимизации w предназначена для представления части системы обучения, которая должна быть адаптирована в качестве реакции на наблюдение событий <tex>z</tex>, происходящих в реальном мире. Функция потерь <tex>Q(z, w)</tex> измеряет производительность системы обучения с параметром <tex>w</tex> при обстоятельствах, описанных событием <tex>z</tex>. |
| + | События <tex>z</tex> моделируются как случайные независимые наблюдения, взятые из неизвестного распределения вероятности <tex>\mathrm{d}P(z)</tex>. Функция риска <tex>J(w)</tex> - это ожидание функции потерь <tex>Q(z, w)</tex> для фиксированного значения параметра <tex>w</tex>. | ||
| + | |||
| + | Функция ожидаемого риска <tex>J(w)</tex> не может быть минимизирована напрямую, потому что распределение <tex>\mathrm{d}P(z)</tex> неизвестно. Однако возможно вычислить приближение <tex>J(w)</tex>, используя конечный обучающий набор независимых наблюдений <tex>z_1, z_L</tex>. | ||
| + | |||
| + | <tex> J (w) \thickapprox \hat{J_L}(w) \stackrel{\triangle}{=} \frac{1}{L} \sum_{n=1}^L Q(z_n,w) </tex> | ||
=== Пакетный градиентный спуск (Batch Gradient Descent) === | === Пакетный градиентный спуск (Batch Gradient Descent) === | ||
| + | |||
| + | [[Файл:BatchGradientDescent.PNG|420px|thumb|right|Пакетный градиентный спуск]] | ||
| − | |||
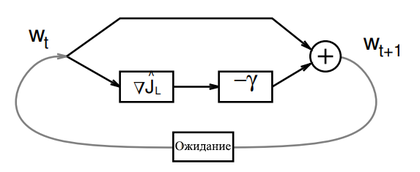
<tex> w_{t+1} = w_t - \gamma_t \bigtriangledown_w \hat{J_L}(w_t) = w_t - \gamma_t\ \frac{1}{L} \sum_{i=1}^L \bigtriangledown_w\ Q(z_i,w_t)\ </tex> | <tex> w_{t+1} = w_t - \gamma_t \bigtriangledown_w \hat{J_L}(w_t) = w_t - \gamma_t\ \frac{1}{L} \sum_{i=1}^L \bigtriangledown_w\ Q(z_i,w_t)\ </tex> | ||
| − | |||
| − | |||
=== Градиентный спуск в реальном времени (Online Gradient Descent) === | === Градиентный спуск в реальном времени (Online Gradient Descent) === | ||
[[Файл:OnlineGradientDescent.PNG|420px|thumb|right|Градиентный спуск в реальном времени]] | [[Файл:OnlineGradientDescent.PNG|420px|thumb|right|Градиентный спуск в реальном времени]] | ||
| + | |||
| + | |||
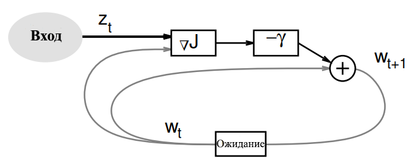
| + | <tex> w_{t+1} = w_t - \gamma_t \bigtriangledown_w Q(z_t, w_t) \ </tex> | ||
| + | |||
| + | |||
| + | |||
| + | <tex> C(w) \stackrel{\triangle}{=} E_z Q(z,w) \stackrel{\triangle}{=} \int Q(z, w)\,\mathrm{d}P(z)\ </tex> | ||
| + | |||
| + | |||
| + | |||
| + | <tex> w_{t+1} = w_t - \gamma_t H(z_t, w_t) \ </tex> | ||
| + | |||
| + | |||
| + | |||
| + | <tex> E_z H(z, w) = \bigtriangledown_w C(w) \ </tex> | ||
== Примеры == | == Примеры == | ||
Версия 21:46, 20 апреля 2020
Обучение в реальном времени, онлайн-обучение (англ. online machine learning) — вид машинного обучения, при котором данные поступают в последовательном порядке и используются для обновления лучшего предсказания на каждом шаге.
Общая информация
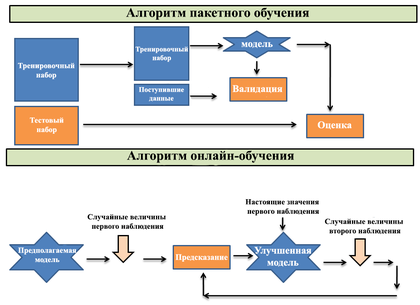
Алгоритмы пакетного обучения обладают рядом критических недостатков из-за необходимости обучать модель с нуля при получении новых данных: низкая эффективность по времени и памяти, плохая масштабируемость для крупных систем. Онлайн-обучение преодолевает эти проблемы, поскольку модель обновляется на основе поступающих в каждый момент времени данных. Благодаря этому, алгоритмы онлайн-обучения гораздо более эффективны в приложениях, где данные не только имеют большой размер, но и поступают с высокой скоростью.
При онлайн-обучении для построения модели необходим один проход по данным, что позволяет не сохранять их для последующего доступа в процессе обучения и использовать меньший объем памяти. Обработка одного объекта за раз также значительно упрощает реализацию алгоритма онлайн-обучения. Однако изменение вида входных данных, выход сервера из строя и многие другие причины могут привести к прекращению корректной работы системы. Оценить качество работы системы при онлайн-обучении сложнее, чем при пакетном: не возможности получить репрезентативный тестовый набор данных.
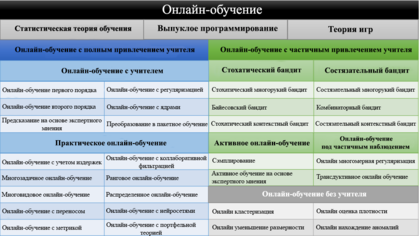
В зависимости от типа обратной связи существующие методы онлайн-обучения можно разделить на три группы:
- Онлайн-обучение с учителем (англ. supervised online learning)
- Онлайн-обучение с частичным привлечением учителя (англ. online learning with limited feedback)
- Онлайн-обучение без учителя (англ. unsupervised online learning)
Математическая основа
Функция ожидаемого риска (Expected Risk Function)
Цель системы обучения состоит в поиске минимум функции , называемой функцией ожидаемого риска. Эта функция раскладывается следующим образом:
Переменная минимизации w предназначена для представления части системы обучения, которая должна быть адаптирована в качестве реакции на наблюдение событий , происходящих в реальном мире. Функция потерь измеряет производительность системы обучения с параметром при обстоятельствах, описанных событием .
События моделируются как случайные независимые наблюдения, взятые из неизвестного распределения вероятности . Функция риска - это ожидание функции потерь для фиксированного значения параметра .
Функция ожидаемого риска не может быть минимизирована напрямую, потому что распределение неизвестно. Однако возможно вычислить приближение , используя конечный обучающий набор независимых наблюдений .
Пакетный градиентный спуск (Batch Gradient Descent)
Градиентный спуск в реальном времени (Online Gradient Descent)