Модели клеточных автоматов — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(intital commit)
 
(Basic defintions, references, wireworld definition, states&rules)
Строка 1: Строка 1:
 +
= Базовые определения =
 +
{{Определение
 +
|id=moore_neighborhood
 +
|definition=
 +
'''Окрестность Мура''' ячейки — совокупность ячеек в сетке (двумерном паркете, трёхмерном Евклидовом пространстве, разбитом на равновеликие кубы), имеющих общую вершину с данной ячейкой.<br>
 +
Окрестность Мура порядка <tex>r</tex> — множество клеток, расстояние Чебышёва<ref>Расстояние Чебышёва URL: https://ru.wikipedia.org/wiki/Расстояние_Чебышёва</ref> до которых от данной клетки не превышает <tex>r</tex>.<br>
 +
Окрестность Мура порядка <tex>r</tex> в двумерном случае представляет собой квадрат со стороной <tex>2r + 1</tex><ref>Weisstein, Eric W. Moore Neighborhood. URL: https://mathworld.wolfram.com/MooreNeighborhood.html</ref>.
 +
}}
 +
 
= Игра "Жизнь" =
 
= Игра "Жизнь" =
  
 
= Коды Вольфрама =
 
= Коды Вольфрама =
 +
 +
= Wireworld =
 +
{{Определение
 +
|definition=
 +
Клеточный автомат '''Wireworld'''<ref>Трофимов Д., Наумов Л. Реализация клеточного автомата WireWorld с помощью инструментального средства CAME&L и его зональная оптимизация, 2007. URL: http://is.ifmo.ru/works/wireworld/</ref> представляет собой синхронный автомат с двумерной решеткой из квадратов, каждая клетка которой может находиться в одном из четырех состояний.
 +
}}
 +
 +
== Состояния ==
 +
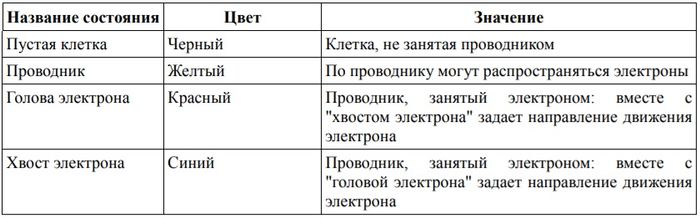
[[Файл:Wireworld_states_meaning_table.jpg|500px|700px|thumb|center|Состояния автомата Wireworld]]
 +
 +
== Правила ==
 +
На каждом шаге автомата ко всем клеткам применяются следующие правила:
 +
# Пустая клетка остается пустой.
 +
# Клетка, находящаяся в состоянии "голова электрона" переходит в состояние "хвост электрона".
 +
# Клетка, находящаяся в состоянии "хвост электрона" переходит в состояние "проводник".
 +
# Клетка, находящаяся в состоянии "проводник" переходит в состояние "голова электрона", в том случае, если среди соседних клеток ровно одна или две находятся в состоянии "голова электрона". Во всех остальных случаях "проводник" остается "проводником".
 +
<br>
 +
При применении данных правил используется [[#moore_neighborhood | окрестность Мура]] – считается, что с данной
 +
клеткой соседствуют все восемь ее непосредственных соседей.
 +
 +
== Общие закономерности ==
 +
Электрон передвигается со скоростью одна клетка за шаг. Если по проводу навстречу идут два электрона, при столкновении они исчезают. При достижении электроном разветвления проводов по каждому из направлений, кроме исходного, уходит по электрону. Если к разветвлению одновременно подходит <tex>2</tex> и более электронов, все они исчезают. При толщине провода в <tex>2</tex> клетки поведение электронов аналогично обычному, при большей толщине поведение становится хаотичным.
 +
 +
== Основные элементы ==
 +
  
 
= См.также =
 
= См.также =
Строка 7: Строка 41:
 
* [[Машина Тьюринга]]
 
* [[Машина Тьюринга]]
 
* [[Линейный ограниченный автомат]]
 
* [[Линейный ограниченный автомат]]
 +
* [https://ru.wikipedia.org/wiki/Автомат_фон_Неймана Автомат фон Неймана]
 +
* [https://ru.wikipedia.org/wiki/%D0%9C%D1%83%D1%80%D0%B0%D0%B2%D0%B5%D0%B9_%D0%9B%D1%8D%D0%BD%D0%B3%D1%82%D0%BE%D0%BD%D0%B0 Муравей Лэнгтона]
  
 
= Литература =
 
= Литература =

Версия 14:01, 24 июня 2020

Базовые определения

Определение:
Окрестность Мура ячейки — совокупность ячеек в сетке (двумерном паркете, трёхмерном Евклидовом пространстве, разбитом на равновеликие кубы), имеющих общую вершину с данной ячейкой.

Окрестность Мура порядка [math]r[/math] — множество клеток, расстояние Чебышёва[1] до которых от данной клетки не превышает [math]r[/math].

Окрестность Мура порядка [math]r[/math] в двумерном случае представляет собой квадрат со стороной [math]2r + 1[/math][2].


Игра "Жизнь"

Коды Вольфрама

Wireworld

Определение:
Клеточный автомат Wireworld[3] представляет собой синхронный автомат с двумерной решеткой из квадратов, каждая клетка которой может находиться в одном из четырех состояний.


Состояния

Состояния автомата Wireworld

Правила

На каждом шаге автомата ко всем клеткам применяются следующие правила:

  1. Пустая клетка остается пустой.
  2. Клетка, находящаяся в состоянии "голова электрона" переходит в состояние "хвост электрона".
  3. Клетка, находящаяся в состоянии "хвост электрона" переходит в состояние "проводник".
  4. Клетка, находящаяся в состоянии "проводник" переходит в состояние "голова электрона", в том случае, если среди соседних клеток ровно одна или две находятся в состоянии "голова электрона". Во всех остальных случаях "проводник" остается "проводником".


При применении данных правил используется окрестность Мура – считается, что с данной клеткой соседствуют все восемь ее непосредственных соседей.

Общие закономерности

Электрон передвигается со скоростью одна клетка за шаг. Если по проводу навстречу идут два электрона, при столкновении они исчезают. При достижении электроном разветвления проводов по каждому из направлений, кроме исходного, уходит по электрону. Если к разветвлению одновременно подходит [math]2[/math] и более электронов, все они исчезают. При толщине провода в [math]2[/math] клетки поведение электронов аналогично обычному, при большей толщине поведение становится хаотичным.

Основные элементы

См.также

Литература

  1. ↑ Расстояние Чебышёва URL: https://ru.wikipedia.org/wiki/Расстояние_Чебышёва
  2. ↑ Weisstein, Eric W. Moore Neighborhood. URL: https://mathworld.wolfram.com/MooreNeighborhood.html
  3. ↑ Трофимов Д., Наумов Л. Реализация клеточного автомата WireWorld с помощью инструментального средства CAME&L и его зональная оптимизация, 2007. URL: http://is.ifmo.ru/works/wireworld/
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Модели_клеточных_автоматов&oldid=74623»