Детерминированные автоматы с магазинной памятью — различия между версиями
Kirillova (обсуждение | вклад) (изменены определения) |
|||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | + | <b> Автоматом с магазинной памятью </b> называется набор <tex> A = \langle\Sigma,Q,s\in Q, \Gamma, Z_0 \in \Gamma, T \subset Q, \delta : Q \times \Sigma \cup \{\varepsilon\} \times \Gamma \rightarrow \cal P</tex><tex>(Q \times \Gamma^*)\rangle </tex>, где <br> | |
| + | * <tex>\Sigma</tex>: конечное множество входных символов. | ||
* <tex>Q</tex>: конечное множество состояний. | * <tex>Q</tex>: конечное множество состояний. | ||
| − | * <tex> | + | * <tex>s</tex>: начальное состояние. |
* <tex>\Gamma</tex>: конечный магазинный алфавит {{---}} множество символов, которые можно помещать в магазин. | * <tex>\Gamma</tex>: конечный магазинный алфавит {{---}} множество символов, которые можно помещать в магазин. | ||
| + | * <tex>Z_0</tex>: начальный магазинный символ (маркер дна). Находится в магазине в начале работы автомата. | ||
| + | * <tex>T</tex>: множество допускающих состояний. | ||
* <tex>\delta</tex>: функция переходов. <tex>\delta (q,a,X)=(p,\gamma)</tex>, где | * <tex>\delta</tex>: функция переходов. <tex>\delta (q,a,X)=(p,\gamma)</tex>, где | ||
** <tex>q</tex>: текущее состояние из Q. | ** <tex>q</tex>: текущее состояние из Q. | ||
| Строка 11: | Строка 14: | ||
** <tex>p</tex>: новое состояние из Q. | ** <tex>p</tex>: новое состояние из Q. | ||
** <tex>\gamma</tex>: цепочка магазинных символов, <i>замещающих</i> <tex>X</tex> на вершине магазина. | ** <tex>\gamma</tex>: цепочка магазинных символов, <i>замещающих</i> <tex>X</tex> на вершине магазина. | ||
| − | |||
| − | |||
| − | |||
}} | }} | ||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | + | <b>Детерменированным автоматом с магазинной памятью</b> называется автомат с магазинной памятью, для которого выполнены следующие условия: | |
| − | #<tex>\ | + | #<tex>\mathcal8 q \in Q, a \in \Sigma \cup \{ \varepsilon \}, X \in \Gamma \Rightarrow \delta(q, a, X)</tex> имеет не более одного элемента. |
#Если <tex>\delta (q,a,X)</tex> непусто для некоторого <tex>a \in \Sigma</tex>, то <tex>\delta (q,\epsilon,X)</tex> должно быть пустым. | #Если <tex>\delta (q,a,X)</tex> непусто для некоторого <tex>a \in \Sigma</tex>, то <tex>\delta (q,\epsilon,X)</tex> должно быть пустым. | ||
}} | }} | ||
| Строка 24: | Строка 24: | ||
==Пример== | ==Пример== | ||
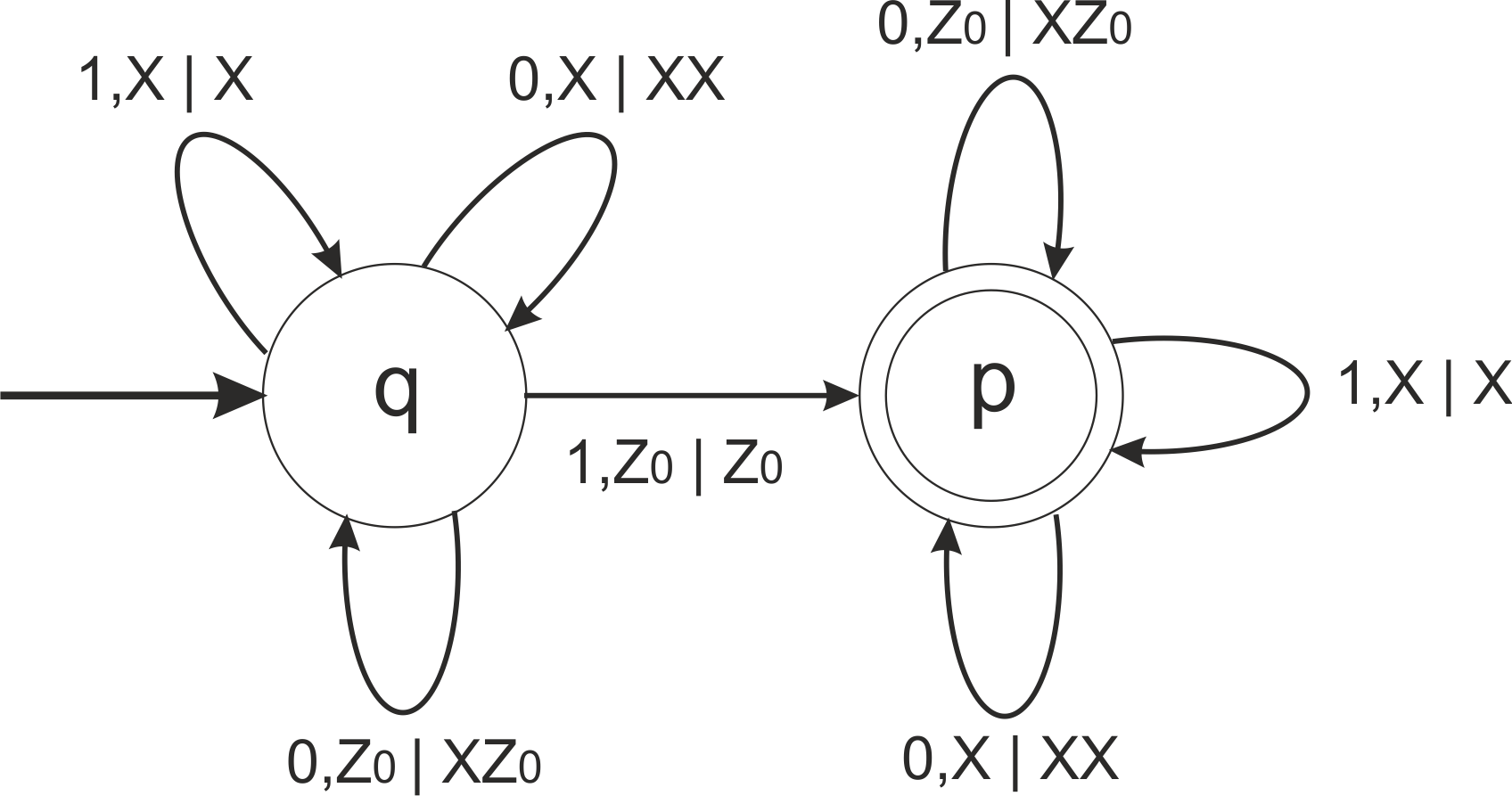
| − | Автомат <tex> | + | Автомат <tex>A=(\{0,1\},\{q,p\},q, \{Z_0,X\}, Z_0,\{p\}, \delta)</tex> с функией перехода <tex>\delta</tex>: |
# <tex>\delta(q,0,Z_0)=(q,XZ_0)</tex> | # <tex>\delta(q,0,Z_0)=(q,XZ_0)</tex> | ||
# <tex>\delta(q,0,X)=(q,XX)</tex> | # <tex>\delta(q,0,X)=(q,XX)</tex> | ||
Версия 00:27, 2 декабря 2011
| Определение: |
Автоматом с магазинной памятью называется набор , где
|
| Определение: |
Детерменированным автоматом с магазинной памятью называется автомат с магазинной памятью, для которого выполнены следующие условия:
|
Будем обозначать переход автомата из состояния в состояние как . Переход автомата из состояния в состояние через промежуточных состояний обозначаем .
Пример
Автомат с функией перехода :