Встречное дерево Фенвика — различия между версиями
Proshev (обсуждение | вклад) |
Proshev (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
Вспомним, что <tex>h(i)</tex> возвращает количество единиц в двоичной записи числа <tex>i</tex>, а каждый столбец оригинального дерево Фенвика вычисляется по формуле <tex>F(i) = \sum_{j=i-2^{h(i)}+1}^i a[j]</tex> | Вспомним, что <tex>h(i)</tex> возвращает количество единиц в двоичной записи числа <tex>i</tex>, а каждый столбец оригинального дерево Фенвика вычисляется по формуле <tex>F(i) = \sum_{j=i-2^{h(i)}+1}^i a[j]</tex> | ||
| + | |||
| + | И если оригинальное дерево выглядело подобным образом: | ||
| + | |||
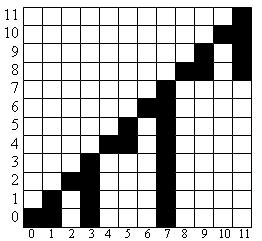
| + | [[Файл:Bit.jpg|thumb|300px|По горизонтали - содержимое массива T,<br/> по вертикали - содержимое массива A]] | ||
| + | |||
| + | То встречное дерево Фенвика выглядит вот так: | ||
Версия 05:20, 2 мая 2011
| Определение: |
| Встречное дерево Фенвика — дерево Фенвика, в котором над каждым столбцом идет столбец такой же высоты, вычисляемый по формуле . |
Вспомним, что возвращает количество единиц в двоичной записи числа , а каждый столбец оригинального дерево Фенвика вычисляется по формуле
И если оригинальное дерево выглядело подобным образом:
То встречное дерево Фенвика выглядит вот так: