Реализация запроса в дереве отрезков снизу

Описание

Реализация запроса снизу вверх в дереве отрезков является, в отличие от реализации сверху вниз, итеративным методом.

Алгоритм

Реализация запроса снизу вверх

Будем рассматривать дерево отрезков с операцией нахождения минимального значения на отрезке(RMQ).
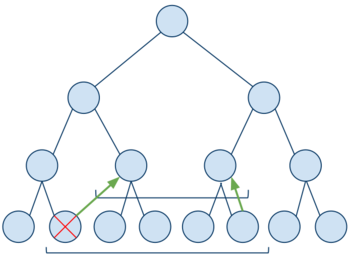
Если левая граница является правым сыном, то отрезаем ее и аналогично рассматриваем правую границу (является ли правая граница левым сыном). Затем поднимаемся к родителям новых границ. Отрезая границу, мы считаем минимум из отрезанного значения и минимума на оставшемся отрезке.

Псевдокод

Псевдокод функции нахождения минимума на отрезке [math][left, right][/math].

  segmentMin(left, right)
     res = MAX_INT; 
     while left < right
        if left == <правый сын>
           res = min(result, data[left]);
           left = parent(left + 1);
        else
           left = parent(left);
        if right == <левый сын>
           result = min(result, data[right]);
           right = parent(right - 1);
        else
           right = parent(right);
        if left == right
           result = min(result, data[left]);
        return result;

Функция [math]parent()[/math] возвращает родителя аргумента.

Ссылки

MAXimal :: algo :: Дерево отрезков

Дерево отрезков — Википедия

Визуализатор

Алгоритм