Открытое и закрытое хеширование — различия между версиями
Baev.dm (обсуждение | вклад) (→Открытое хеширование) |
Baev.dm (обсуждение | вклад) (→Закрытое хеширование) |
||
| Строка 7: | Строка 7: | ||
В случае метода открытой адресации (или по-другому: метод закрытого хеширования) все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличии от хеширования с цепочками, при использовании метода открытой адресации может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, так что будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой. | В случае метода открытой адресации (или по-другому: метод закрытого хеширования) все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличии от хеширования с цепочками, при использовании метода открытой адресации может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, так что будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой. | ||
Для разрешения же коллизий применяются несколько подходов. Самый простой из них – это метод линейного исследования. В этом случае при возникновении коллизии следующие за текущей ячейки проверяются одна за другой, пока не найдётся пустая ячейка, куда и помещается наш элемент. Так, при достижении последнего индекса таблицы, мы перескакиваем в начало, рассматривая её как «цикличный» массив. | Для разрешения же коллизий применяются несколько подходов. Самый простой из них – это метод линейного исследования. В этом случае при возникновении коллизии следующие за текущей ячейки проверяются одна за другой, пока не найдётся пустая ячейка, куда и помещается наш элемент. Так, при достижении последнего индекса таблицы, мы перескакиваем в начало, рассматривая её как «цикличный» массив. | ||
| − | [[Файл: | + | [[Файл:Hash_close_new.jpg|375px|thumb|center|Закрытое хеширование с использованием метода линейного исследования]] |
Одной из сложных вопросов реализации хеширования с открытой адресацией – это операция удаления элемента. Дело в том, что если мы просто удалим некий элемент их хеш-таблицы, то сделаем невозможным поиск ключа, в процессе вставки которого текущая ячейка оказалась заполненной. Так, мы можем помечать очищенные ячейки какой-то меткой, чтобы впоследствии это учитывать. (Анализ закрытого хеширования см. Т.Корман, второе издание, стр. 305) | Одной из сложных вопросов реализации хеширования с открытой адресацией – это операция удаления элемента. Дело в том, что если мы просто удалим некий элемент их хеш-таблицы, то сделаем невозможным поиск ключа, в процессе вставки которого текущая ячейка оказалась заполненной. Так, мы можем помечать очищенные ячейки какой-то меткой, чтобы впоследствии это учитывать. (Анализ закрытого хеширования см. Т.Корман, второе издание, стр. 305) | ||
| + | |||
==См. также== | ==См. также== | ||
* [[Различные алгоритмы хеширования]] | * [[Различные алгоритмы хеширования]] | ||
Версия 21:00, 17 мая 2011
Есть разные методы борьбы с коллизиями. Рассмотрим два из них.
Открытое хеширование
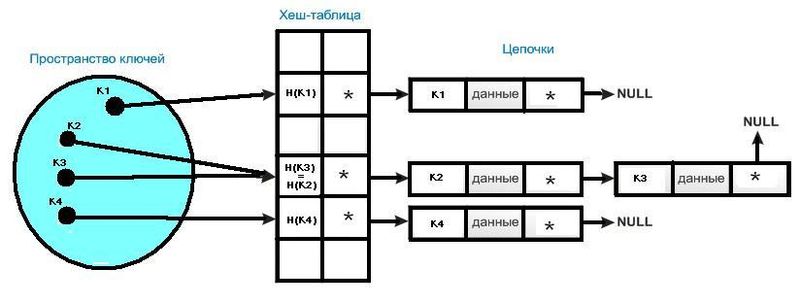
Открытое хеширование (или по-другому: метод цепочек) — простейший метод борьбы с коллизиями. При использовании этого метода мы объединяем все элементы, хешированные в одну и ту же ячейку, в связный список. Ячейка содержит указатель на заголовок списка всех элементов, хэш-значение ключа которых равно ; если таких элементов нет, ячейка содержит значение . Элементы вставляются в заголовок списка. Время, необходимое для вставки в наихудшем случае равно , учитывая то, что мы предполагаем отсутствие вставляемого элемента в таблице. Время поиска зависит от длины списка, и в худшем случае равно . Эта ситуация, когда все элементы хешируются в единственную ячейку. Если функция распределяем ключей по ячейкам таблицы равномерно, то в каждом списке будет содержаться порядка ключей. Это число называется коэффициентом заполнения хеш-таблицы. Математический анализ хеширования с цепочками показывает, что в среднем случае все операции в такой хеш-таблице в среднем выполняются за время . (Анализ открытого хеширования см. Т.Корман, второе издание, стр. 288)
Закрытое хеширование
В случае метода открытой адресации (или по-другому: метод закрытого хеширования) все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличии от хеширования с цепочками, при использовании метода открытой адресации может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, так что будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой. Для разрешения же коллизий применяются несколько подходов. Самый простой из них – это метод линейного исследования. В этом случае при возникновении коллизии следующие за текущей ячейки проверяются одна за другой, пока не найдётся пустая ячейка, куда и помещается наш элемент. Так, при достижении последнего индекса таблицы, мы перескакиваем в начало, рассматривая её как «цикличный» массив.
Одной из сложных вопросов реализации хеширования с открытой адресацией – это операция удаления элемента. Дело в том, что если мы просто удалим некий элемент их хеш-таблицы, то сделаем невозможным поиск ключа, в процессе вставки которого текущая ячейка оказалась заполненной. Так, мы можем помечать очищенные ячейки какой-то меткой, чтобы впоследствии это учитывать. (Анализ закрытого хеширования см. Т.Корман, второе издание, стр. 305)
См. также
Литература
- Т. Кормен, Ч. Лейзерсон, Р. Ривест: Алгоритмы: построение и анализ, 2-е изд