Хеширование

Хеширование - класс методов поиска идея которого состоит в использовании некоторой частичной информации, полученной из ключа(однозначно характеризующего элемент), в качестве основы поиска.С помощью хеш-функции мы вычисляем хеш-код и используем его для проведения поиска.Если у двух элементов хеш-коды разные, элементы гарантированно различаются; если одинаковые — элементы, скорее всего, одинаковы. В общем случае однозначного соответствия между исходными данными и хеш-кодом нет в силу того, что количество значений хеш-функций меньше, чем вариантов исходных данных; существует элементы, дающие одинаковые хеш-коды — так называемые коллизии. Вероятность возникновения коллизий играет немаловажную роль в оценке качества хеш-функций.

Хеш - таблица

Хеш-табли́ца — это структура данных, реализующая интерфейс ассоциативного массива, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.

Введение

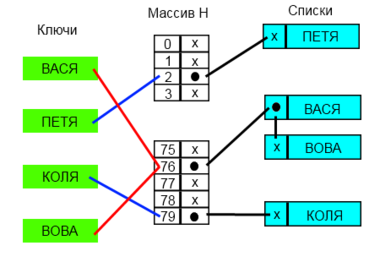
Существует два основных варианта хеш-таблиц: с цепочками и открытой адресацией. Хеш-таблица содержит некоторый массив [math]H[/math], элементы которого есть пары (хеш-таблица с открытой адресацией) или списки пар (хеш-таблица с цепочками).

Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение [math]i = hash(key)[/math] играет роль индекса в массиве [math]H[/math]. Затем выполняемая операция (добавление, удаление или поиск) перенаправляется объекту, который хранится в соответствующей ячейке массива [math]H[i][/math].

Ситуация, когда для различных ключей получается одно и то же хеш-значение, называется коллизией. Такие события не так уж и редки — например, при вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии уже превысит 50 % (если каждый элемент может равновероятно попасть в любую ячейку). Поэтому механизм разрешения коллизий — важная составляющая любой хеш-таблицы.

В некоторых специальных случаях удаётся избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую совершенную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий. Хеш-таблицы, использующие подобные хеш-функции, не нуждаются в механизме разрешения коллизий, и называются хеш-таблицами с прямой адресацией.

Число хранимых элементов, делённое на размер массива [math]H[/math] (число возможных значений хеш-функции), называется коэффициентом заполнения хеш-таблицы (load factor) и является важным параметром, от которого зависит среднее время выполнения операций.

Свойства хеш-таблицы

Важное свойство хеш-таблиц состоит в том, что, при некоторых разумных допущениях, все три операции (поиск, вставка, удаление элементов) в среднем выполняются за время [math]O(1)[/math]. Но при этом не гарантируется, что время выполнения отдельной операции мало́. Это связано с тем, что при достижении некоторого значения коэффициента заполнения необходимо осуществлять перестройку индекса хеш-таблицы: увеличить значение размера массива [math]H[/math] и заново добавить в пустую хеш-таблицу все пары.

Разрешение коллизий

Существует несколько способов разрешения коллизий.

Открытое хеширование

Разрешение коллизий при помощи цепочек.

Каждая ячейка массива [math]H[/math] является указателем на связный список(цепочку) пар ключ-значение, соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются списки длиной более одного элемента.

Операции поиска или удаления элемента требуют просмотра всех элементов соответствующему ему списка, чтобы найти в нем элемент с заданным ключом. Для добавления элемента нужно добавить элемент в конец или начало соответствующего списка, и, в случае, если коэффициент заполнения станет слишком велик, увеличить размер массива [math]H[/math] и перестроить таблицу.

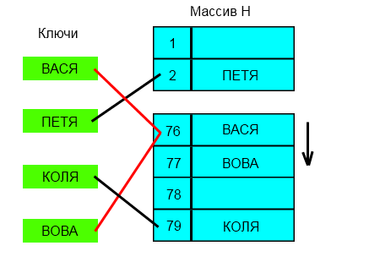
Закрытое хеширование

Пример хеш-таблицы с открытой адресацией и линейным пробированием.

В массиве [math]H[/math] хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива [math]H[/math] в некотором порядке до тех пор, пока не будет найдена первая свободная ячейка, в которую и будет записан новый элемент. Этот порядок вычисляется на лету, что позволяет сэкономить на памяти для указателей, требующихся в хеш-таблицах с цепочками.

Последовательность, в которой просматриваются ячейки хеш-таблицы, называется последовательностью проб. В общем случае, она зависит только от ключа элемента, то есть это последовательность [math]h_0(x)[/math], [math]h_1(x)[/math], ...,[math]h_n[/math][math]_-[/math][math]_1[/math][math](x)[/math], где [math]x[/math] — ключ элемента, а [math]h_i(x)[/math] — произвольные функции, сопоставляющие каждому ключу ячейку в хеш-таблице. Первый элемент в последовательности, как правило, равен значению некоторой хеш-функции от ключа, а остальные считаются от него каким-нибудь способом. Для успешной работы алгоритмов поиска последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.

Алгоритм поиска просматривает ячейки хеш-таблицы в том же самом порядке, что и при вставке, до тех пор, пока не найдется либо элемент с искомым ключом, либо свободная ячейка (что означает отсутствие элемента в хеш-таблице).

Удаление элементов в такой схеме несколько затруднено. Обычно поступают так: заводят булевый флаг для каждой ячейки, помечающий, удален ли элемент в ней или нет. Тогда удаление элемента состоит в установке этого флага для соответствующей ячейки хеш-таблицы, но при этом необходимо модифицировать процедуру поиска существующего элемента так, чтобы она считала удалённые ячейки занятыми, а процедуру добавления — чтобы она их считала свободными и сбрасывала значение флага при добавлении.

Источники

• Дональд Кнут "Искусство программирования" Хеширование
• Хеширование
• Хеш-таблица