Лемма о единственном паросочетании в графе замен — различия между версиями
DrozdovVA (обсуждение | вклад) (Новая страница: «{{Лемма |about= о единственном паросочетании графе замен |statement= Дан [[Определение матроида|мат…») |
DrozdovVA (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
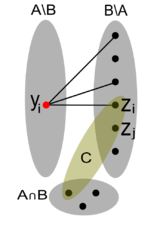
Заметим, что т. к. в графе <tex>G_M(A)</tex> нет другого паросочетания, то в нем нет циклов четной длины, значит, граф является ациклическим. Упорядочим вершины левой <tex>(y_i \in A \setminus B)</tex> и правой <tex>(z_j \in B \setminus A)</tex> долей таким образом, что <tex>\forall j < i : (y_i z_j) \notin G_M(A)</tex>. Заметим также, что при такой ориентации ребра паросочетания имеют вид <tex>(y_i z_i)</tex>. Действительно, ребро в первую вершину правой доли может идти только из первой вершины левой доли. Аналогично во вторую вершину правой доли ведет ребро из второй вершины левой доли и, возможно, ребро из первой вершины, которое уже не может быть использовано в паросочетании и т. д. | Заметим, что т. к. в графе <tex>G_M(A)</tex> нет другого паросочетания, то в нем нет циклов четной длины, значит, граф является ациклическим. Упорядочим вершины левой <tex>(y_i \in A \setminus B)</tex> и правой <tex>(z_j \in B \setminus A)</tex> долей таким образом, что <tex>\forall j < i : (y_i z_j) \notin G_M(A)</tex>. Заметим также, что при такой ориентации ребра паросочетания имеют вид <tex>(y_i z_i)</tex>. Действительно, ребро в первую вершину правой доли может идти только из первой вершины левой доли. Аналогично во вторую вершину правой доли ведет ребро из второй вершины левой доли и, возможно, ребро из первой вершины, которое уже не может быть использовано в паросочетании и т. д. | ||
| − | Требуется доказать, что <tex>B</tex> независимо. Предположим обратное. Пусть <tex>B \notin I</tex>, тогда существует [[Теорема о циклах|цикл]] <tex>C \subset B</tex>.<br/> Выберем минимальное <tex>i</tex> такое, что <tex>C \subset (A \cap B) \cup \{z_1..z_i\}</tex>. Т. к. <tex>\forall j < i : (y_i z_j) \notin G_M(A)</tex>, то <tex>A \setminus y_i \cup z_j \notin I</tex>, следовательно, <tex>C \setminus z_i \subset \langle A \setminus y_i \rangle </tex>. По [[Оператор замыкания для матроидов#theorem|свойствам замыкания 1 и | + | Требуется доказать, что <tex>B</tex> независимо. Предположим обратное. Пусть <tex>B \notin I</tex>, тогда существует [[Теорема о циклах|цикл]] <tex>C \subset B</tex>.<br/> Выберем минимальное <tex>i</tex> такое, что <tex>C \subset (A \cap B) \cup \{z_1..z_i\}</tex>. Т. к. <tex>\forall j < i : (y_i z_j) \notin G_M(A)</tex>, то <tex>A \setminus y_i \cup z_j \notin I</tex>, следовательно, <tex>C \setminus z_i \subset \langle A \setminus y_i \rangle </tex>. По [[Оператор замыкания для матроидов#theorem|свойствам замыкания 1 и 3]] получаем:<br/> |
<tex>C \setminus z_i \subset \langle A \setminus y_i \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle \langle A \setminus y_i \rangle \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex> <br/> | <tex>C \setminus z_i \subset \langle A \setminus y_i \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle \langle A \setminus y_i \rangle \rangle \Rightarrow \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex> <br/> | ||
Т.к. <tex>z_i \in \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex>, то <tex>A \setminus y_i \cup z_i \notin I</tex>, т. е. в <tex>G_M(A)</tex> не существует ребра <tex>(y_i z_i)</tex>. Но тогда, как было отмечено ранее, не существует полного паросочетания. Получили противоречие. | Т.к. <tex>z_i \in \langle C \setminus z_i \rangle \subset \langle A \setminus y_i \rangle</tex>, то <tex>A \setminus y_i \cup z_i \notin I</tex>, т. е. в <tex>G_M(A)</tex> не существует ребра <tex>(y_i z_i)</tex>. Но тогда, как было отмечено ранее, не существует полного паросочетания. Получили противоречие. | ||
}} | }} | ||
Версия 00:45, 10 июня 2011
| Лемма (о единственном паросочетании графе замен): |
Дан матроид . Пусть двудольный граф содержит единственное полное паросочетание на , где и . Тогда . |
| Доказательство: |
|
Заметим, что т. к. в графе нет другого паросочетания, то в нем нет циклов четной длины, значит, граф является ациклическим. Упорядочим вершины левой и правой долей таким образом, что . Заметим также, что при такой ориентации ребра паросочетания имеют вид . Действительно, ребро в первую вершину правой доли может идти только из первой вершины левой доли. Аналогично во вторую вершину правой доли ведет ребро из второй вершины левой доли и, возможно, ребро из первой вершины, которое уже не может быть использовано в паросочетании и т. д. Требуется доказать, что независимо. Предположим обратное. Пусть , тогда существует цикл . |