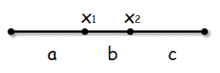Поиск с помощью золотого сечения — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
{{В разработке}} | {{В разработке}} | ||
| − | '''Поиск с помощью золотого сечения''' (''Golden section search'') - это улучшение наивной реализации троичного поиска, служащий для поиска минимума/максимума функции. При простом троичном поиске на каждой итерации функция вычисляется в двух точках. Метод же золотого сечения требует вычисления лишь в одной точке (за исключением первой итерации). За счет этого достигается выйгрыш в производительности. | + | '''Поиск с помощью золотого сечения''' (''Golden section search'') - это улучшение наивной реализации [[Троичный поиск|троичного поиска]], служащий для поиска минимума/максимума функции. При простом троичном поиске на каждой итерации функция вычисляется в двух точках. Метод же золотого сечения требует вычисления лишь в одной точке (за исключением первой итерации). За счет этого достигается выйгрыш в производительности. |
==Алгоритм== | ==Алгоритм== | ||
| − | + | Рассмотрим одну итерацию алгоритма троичного поиска. Попробуем подобрать такое разбиение отрезка на три части, чтобы на следующей итерации одна из точек нового разбиения совпала с одной из точек текущего разбиения. Тогда в следующий раз не придется считать функцию в двух точках, так как в одной она уже была посчитана. | |
| + | |||
| + | [[Файл:Goldensection.gif|220px]] | ||
| + | |||
| + | Точки <tex>x_1</tex> и <tex>x_2</tex> разбивают отрезок на три части. Потребуем, чтобы одновременно выполнялось: | ||
| + | |||
| + | <tex> \frac{a + b}{c} = \frac{b + c}{a} = \phi </tex> | ||
| + | |||
| + | <tex> \frac{a}{b} = \phi </tex> | ||
| + | |||
| + | <tex> \frac{c}{b} = \phi </tex> | ||
| + | |||
| + | Где <tex> \phi </tex> - это некоторое отношение, в котором делим отрезок (точки <tex>x_1</tex> и <tex>x_2</tex> разбивают отрезок симметрично). | ||
| + | |||
| + | Тогда: | ||
| + | |||
| + | <tex> a + b = \phi c, a = \phi b, c = \phi b</tex>, откуда получаем <tex> \phi + 1 = \phi^2 \Rightarrow \phi = \frac{1 + \sqrt{5}}{2}</tex> (тот корень уравнения, который меньше нуля, по понятным причнам отбросили) | ||
| + | |||
| + | Это число совпадает с золотым сечением. Отсюда название метода. | ||
| + | |||
| + | |||
===Псевдокод=== | ===Псевдокод=== | ||
| Строка 12: | Строка 32: | ||
==Ссылки== | ==Ссылки== | ||
| − | [http://en.wikipedia.org/wiki/Golden_section_search Wikipedia - Golden section search] | + | [http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%B7%D0%BE%D0%BB%D0%BE%D1%82%D0%BE%D0%B3%D0%BE_%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D1%8F Википедия - Метод золотого сечения] |
| + | |||
| + | [http://en.wikipedia.org/wiki/Golden_section_search Wikipedia - Golden section search] (english) | ||
Версия 10:51, 15 июня 2011
Поиск с помощью золотого сечения (Golden section search) - это улучшение наивной реализации троичного поиска, служащий для поиска минимума/максимума функции. При простом троичном поиске на каждой итерации функция вычисляется в двух точках. Метод же золотого сечения требует вычисления лишь в одной точке (за исключением первой итерации). За счет этого достигается выйгрыш в производительности.
Содержание
Алгоритм
Рассмотрим одну итерацию алгоритма троичного поиска. Попробуем подобрать такое разбиение отрезка на три части, чтобы на следующей итерации одна из точек нового разбиения совпала с одной из точек текущего разбиения. Тогда в следующий раз не придется считать функцию в двух точках, так как в одной она уже была посчитана.
Точки и разбивают отрезок на три части. Потребуем, чтобы одновременно выполнялось:
Где - это некоторое отношение, в котором делим отрезок (точки и разбивают отрезок симметрично).
Тогда:
, откуда получаем (тот корень уравнения, который меньше нуля, по понятным причнам отбросили)
Это число совпадает с золотым сечением. Отсюда название метода.
Псевдокод
Асимптотика
Ссылки
Википедия - Метод золотого сечения
Wikipedia - Golden section search (english)