Вещественный двоичный поиск — различия между версиями
| Строка 8: | Строка 8: | ||
== Решение задачи == | == Решение задачи == | ||
Применим идею двоичного поиска. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это. | Применим идею двоичного поиска. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это. | ||
| + | |||
| + | == Выбор границы == | ||
| + | Для начала найдем правую границу. Выберем произвольную положительную точку (например 1). Будем удваивать ее до тех пор, пока значение функции в этой точке меньше заданного. Для того, чтобы найти левую границу выберем произвольную отрицательную точку. Будем удваивать ее до тех пор, пока значение в ней будет больше заданного значения. | ||
== Способы закончить поиск == | == Способы закончить поиск == | ||
| Строка 20: | Строка 23: | ||
# Итеративный способ. В этом способе выполниться только конечное число число итераций. | # Итеративный способ. В этом способе выполниться только конечное число число итераций. | ||
#* Плюсом этого способа является фиксированная погрешность. | #* Плюсом этого способа является фиксированная погрешность. | ||
| + | |||
| + | == Псевдокод == | ||
| + | double find_left(double c) { | ||
| + | double x = -1; | ||
| + | while (f(x) > c) { | ||
| + | x *= 2; | ||
| + | } | ||
| + | return x; | ||
| + | } | ||
| + | |||
| + | double find_right(double c) { | ||
| + | double x = 1; | ||
| + | while (f(x) < c) { | ||
| + | x *= 2; | ||
| + | } | ||
| + | return x; | ||
| + | } | ||
| + | |||
| + | double bin_search(double c) { | ||
| + | double left = find_left(); | ||
| + | double right = find_right(); | ||
| + | while (left < right - eps) { //Здесь можно поставить другое условие выхода | ||
| + | double m = (left + right) / 2; | ||
| + | if (f(m) < c) | ||
| + | l = m; | ||
| + | else | ||
| + | r = m; | ||
| + | } | ||
| + | return l; | ||
| + | } | ||
Версия 22:19, 15 июня 2011
Вещественный двоичный поиск - алгоритм поиска аргумента для заданного значения монотонной вещественной функции.
Содержание
Формулировка задачи
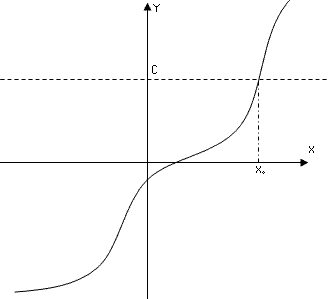
Пусть нам задана монотонная функция. Необходимо найти место, где значение функции становится меньше, чем какое-то заданное значение.
Решение задачи
Применим идею двоичного поиска. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это.
Выбор границы
Для начала найдем правую границу. Выберем произвольную положительную точку (например 1). Будем удваивать ее до тех пор, пока значение функции в этой точке меньше заданного. Для того, чтобы найти левую границу выберем произвольную отрицательную точку. Будем удваивать ее до тех пор, пока значение в ней будет больше заданного значения.
Способы закончить поиск
- Первый способ заключается в том, чтобы остановиться, когда рассматриваемый отрезок станет меньше заданного эпсилон. Но у этого подхода есть свои плюсы и минусы:
- Алгоритм с большой точностью найдет значение аргумента
- Алгоритм может зациклиться. В компьютере мы работаем с конечным числом вещественных чисел. У чисел есть точность. Соответственно при больших значениях функции, длина отрезка может никогда не уменьшиться до заданного значения
- Второй способ менее точен. Предлагается заканчивать алгоритм, когда значение функции на концах отрезках различается менее, чем на заданное эпсилон.
- В отличии от предыдущего, не зацикливается при больших значениях функции.
- Возможна большая погрешность, если функция будет очень медленно возрастать
- Абсолютно точный поиск. Вспомним о том, что вещественный числа в компьютере дискретным. Будем завершать поиск, когда границы отрезка - два соседних по представлению значения в типе данных. Утверждается, что два числа - соседние, если середина их отрезка совпадает или с левой, или с правой границей.
- Возможно плохое поведение, если искомый аргумент равен 0.
- Итеративный способ. В этом способе выполниться только конечное число число итераций.
- Плюсом этого способа является фиксированная погрешность.
Псевдокод
double find_left(double c) {
double x = -1;
while (f(x) > c) {
x *= 2;
}
return x;
}
double find_right(double c) {
double x = 1;
while (f(x) < c) {
x *= 2;
}
return x;
}
double bin_search(double c) {
double left = find_left();
double right = find_right();
while (left < right - eps) { //Здесь можно поставить другое условие выхода
double m = (left + right) / 2;
if (f(m) < c)
l = m;
else
r = m;
}
return l;
}