Точка сочленения, эквивалентные определения — различия между версиями
| Строка 7: | Строка 7: | ||
(2) <b>Точка сочленения</b> графа <tex>G</tex> - вершина, при удалении которой в <tex>G</tex> увеличивается число [[Отношение связности, компоненты связности|компонент связности]]. | (2) <b>Точка сочленения</b> графа <tex>G</tex> - вершина, при удалении которой в <tex>G</tex> увеличивается число [[Отношение связности, компоненты связности|компонент связности]]. | ||
}} | }} | ||
| − | + | [[Файл:Vert.png]] | |
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
Версия 21:38, 25 октября 2011
| Определение: |
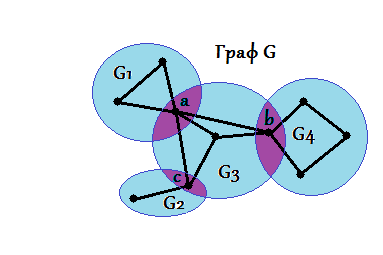
| (1) Точка сочленения графа - вершина, принадлежащая как минимум двум блокам . |
| Определение: |
| (2) Точка сочленения графа - вершина, при удалении которой в увеличивается число компонент связности. |
| Лемма: |
Определения (1) и (2) эквивалентны. |
| Доказательство: |
|
Пусть вершина принадлежит некоторым блокам и . Вершине инцидентны некоторые ребра и . Ребра и находятся в различных блоках, поэтому не существует двух непересекающихся путей между их концами. Учитывая, что один из путей между концами - путь из в эту же вершину, получаем, что любой путь, соединяющий и , пройдет через . При удалении между и не останется путей, и одна из компонент связности распадется на две. Пусть принадлежала только одному блоку . Все вершины , смежные с , также лежат в (в силу рефлексивности отношения вершинной двусвязности). Между каждой парой вершин из существует как минимум два вершинно непересекающихся пути. Теперь удалим . Это разрушит путь , но не разрушит любой оставшийся, так как иначе он тоже прошел бы через . Рассмотрим - компоненту связности, в которой лежала . Пусть между вершинами существовал путь, проходящий через . Но он проходил также через некоторые вершины из , связность которых не нарушилась, поэтому есть как минимум еще один путь, отличный от удаленного. Противоречие: число компонент связности не увеличилось. |
| Теорема: |
Следующие утверждения эквивалентны:
(1) - точка сочленения графа ; (2) существуют такие вершины и , отличные от , что принадлежит любому простому пути из в ; (3) существует разбиение множества вершин на такие два подмножества и , что для любых вершин и вершина принадлежит любому простому пути из в . |
| Доказательство: |
|
Так как - точка сочленения графа , то граф не связен и имеет по крайней мере две компоненты. Образуем разбиение , отнеся к вершины одной из этих компонент, а к - вершины всех остальных компонент. Тогда любые две вершины и лежат в разных компонентах графа . Следовательно, любой простой путь из в графа содержит . Следует из того, что (2) - частный случай (3). Если принадлежит любому простому пути в , соединяющему и , то в нет простого пути, соединяющего эти вершины в . Поскольку не связен, то - точка сочленения графа . |
Литература
- Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009