Эквивалентность состояний ДКА — различия между версиями
(→Проверка эквивалентности автоматов) |
(Какой-то отстой не по теме был написан, все нафиг поудалял, написал нормально) |
||
| Строка 2: | Строка 2: | ||
== Эквивалентность автоматов == | == Эквивалентность автоматов == | ||
| − | < | + | {{Определение |
| + | |definition = Два <em> автомата</em> <tex> \mathcal{A}_1 = \langle Q_1,\Sigma,\delta_1,s_{10}, T_1\subseteq Q_1 \rangle </tex> и <tex>\mathcal{A}_2 = \langle Q_2,\Sigma,\delta_2,s_{20}, T_2\subseteq Q_2 \rangle </tex> называются <em>эквивалентными</em>, если они распознают один и тот же язык над алфавитом <tex>\Sigma</tex>, то есть <tex>\mathcal{L}(\mathcal{A}_1) = \mathcal{L}(\mathcal{A}_2)</tex> | ||
| + | }} | ||
| − | + | {{Определение | |
| − | + | |definition = Слово <tex>z \in \Sigma^*</tex> различает два состояния <tex>q_i</tex> и <tex>q_j</tex>, если | |
| − | + | * <tex> \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow t_1 \notin T \Leftrightarrow t_2 \in T </tex>. | |
| + | }} | ||
| + | |||
| + | {{Определение | ||
| + | |definition = Два <em> состояния</em> <tex>q_i</tex> и <tex>q_j</tex> называются <em>эквивалентными</em> <tex>(q_i \sim q_j)</tex>, если не существует строки, которая их различает, то есть <tex>\forall z\in \Sigma^*</tex> верно, что | ||
| + | * <tex> \langle q_i, z \rangle \vdash^* \langle t_1, \varepsilon \rangle, \langle q_j, z \rangle \vdash^* \langle t_2, \varepsilon \rangle \Rightarrow t_1 \in T \Leftrightarrow t_2 \in T </tex>. | ||
| + | }} | ||
*'''Пример двух эквивалентных автоматов:''' | *'''Пример двух эквивалентных автоматов:''' | ||
| Строка 13: | Строка 21: | ||
<em>Состояния <tex>B</tex> и <tex>C</tex> допускающие.</em> | <em>Состояния <tex>B</tex> и <tex>C</tex> допускающие.</em> | ||
| − | |||
| − | |||
| − | |||
| − | + | == Алгоритм проверки эквивалентности автоматов == | |
| − | |||
| − | |||
| − | |||
== Литература == | == Литература == | ||
| − | |||
Версия 02:45, 14 ноября 2011
Эквивалентность автоматов
| Определение: |
| Два автомата и называются эквивалентными, если они распознают один и тот же язык над алфавитом , то есть |
| Определение: |
Слово различает два состояния и , если
|
| Определение: |
Два состояния и называются эквивалентными , если не существует строки, которая их различает, то есть верно, что
|
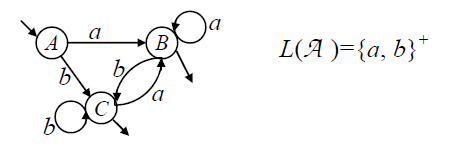
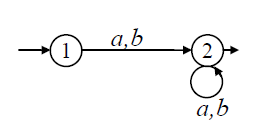
- Пример двух эквивалентных автоматов:
Состояния и допускающие.