Алгоритм Форда-Фалкерсона для поиска максимального паросочетания

Идея алгоритма

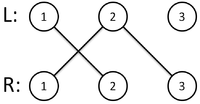
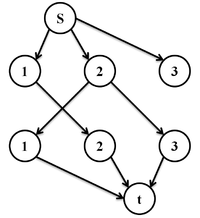
Пусть дан неориентированный двудольный граф [math]G(V, E)[/math] и требуется найти максимальное паросочетание в нём. Обозначим доли исходного графа как

Пример графа G.

Соответствующий граф G'.

[math]L[/math] и [math]R[/math]. Построим граф [math]G'(V', E')[/math] следующим образом:

[math]V' = V \cup \{s, t\}[/math] (т.е. добавим новый исток [math]s[/math] и сток [math]t[/math]);

[math]E' = \{(s, u): u \in L\} \cup \{(u, v): u \in L, v \in R\ , (u, v) \in E\} \cup \{(v, t): v \in R\} [/math].

Изначально текущее паросочетание пусто. На каждом шаге алгоритма будем поддерживать следующий инвариант: в текущее найденное паросочетание входят те и только те ребра, которые направлены из [math]L[/math] в [math]R[/math].

1. Ищем в графе [math]G'[/math] путь из [math]s[/math] в [math]t[/math] поиском в глубину.
2. Если путь найден, перезаписываем текущее паросочетание. Теперь инвертируем все рёбра на пути (ребро [math](u, v)[/math] становится ребром [math](v, u)[/math] ) и удаляем [math](s, L)[/math] и [math](R, t)[/math] ребра, покрывающие вершины, принадлежащие текущему паросочетанию.
3. Если путь не был найден, значит текущее паросочетание является максимальным, и алгоритм завершает работу. Иначе переходим к пункту 1.

Корректность алгоритма

Обозначим как [math]p'[/math] путь из [math]s[/math] в [math]t[/math] без первого и последнего ребра. Пусть он является дополняющей цепью для исходного графа [math]G[/math] и обратно - т.е. любая дополняющая цепь графа [math]G[/math] является путем [math]p'[/math]. Тогда из теоремы — если мы на каждом шаге можем найти новый путь, т.е. находим новую дополняющую цепь, то мы увеличиваем текущее паросочетание. Если путь найти мы уже не можем, значит дополняющих цепей в графе нет и текущее паросочетание — искомое. Осталось доказать, что путь [math]p'[/math] действительно является дополняющей цепью.

Т.к. [math]p'[/math] — путь в двудольном графе, он нечетной длины, в котором вершины не повторяются (т.к. этот путь строится с помощью поиска в глубину). Рассмотрим текущее паросочетание. Мы записывали в него ребра из [math]L[/math] в [math]R[/math], но после этого инвертировали их. Значит, ребра текущего паросочетания сейчас ведут из [math]R[/math] в [math]L[/math]. В таком случае ребра пути [math]p'[/math] можно пронумеровать так, чтобы нечетные ребра были свободными, а четные — покрытыми (что соответствует текущему паросочетанию). Тогда этот путь — дополняющая цепь для графа [math]G[/math], и паросочетание можно перезаписать. Обратно — дополняющая цепь в графе [math]G[/math] это путь нечетной длины из [math]L[/math] в [math]R[/math]. Он начинается в какой-то вершине [math]u \in L\[/math] и заканчивается в вершине [math]v \in R\[/math] (поскольку концевые вершины этого пути должны быть свободны). Нo каждая вершина из [math]L[/math] связана ребром с [math]s[/math] в графе [math]G'[/math], аналогично каждая вершина из [math]R[/math] связана ребром с [math]t[/math]. Тогда любая дополняющая цепь в графе [math]G[/math] является частью пути из [math]s[/math] в [math]t[/math] в графе [math]G'[/math], или, что то же самое, является путем [math]p'[/math]. Отсюда следует, что алгоритм корректен.

Оценка производительности

Поиск в глубину запускается от вершины [math]s[/math] не более чем [math]L[/math] раз, т.к. из [math]s[/math] ведет ровно [math]L[/math] ребер, и при каждом запуске одно из них инвертируется. Сам поиск работает за [math]O(E)[/math], каждая инвертация и перезапись паросочетания так же занимает [math]O(E)[/math] времени. Тогда все время алгоритма ограничено [math]O(VE)[/math].

Псевдокод

В массиве [math]px[/math] хранятся вершины [math]y \in R[/math], инцидентные [math]x_i \in L[/math] в текущем паросочетании, для [math]py[/math] аналогично. Максимальное паросочетание - такие ребра [math](x, y)[/math], что [math]x \in L, y \in R, px[x] == y[/math].

 bool  dfs(x)
   if vis[x]
     return false
   vis[x] = true
   for [math]xy \in E[/math]
     if py[y] = -1
       py[y] = x
       px[x] = y
       return true
     else 
       if dfs(py[y])
         py[y] = x
         px[x] = y
         return true
   return false

 px[] = -1
 py[] = -1
 is_path = true;
 while (is_path)
   is_path = false
   vis[] = false
   for [math]x \in L[/math]
     if (px[x] == -1) 
       if dfs(x)
         is_path = true

Ссылки

• Теорема о максимальном паросочетании и дополняющих цепях
• Алгоритм Форда-Фалкерсона, реализация с помощью поиска в глубину

Литература

Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд "Алгоритмы: построение и анализ", 2-е издание, стр. 758 - 761.