Произвольно вычерчиваемые из заданной вершины графы

Определение:

Граф называется произвольно вычерчиваемым из вершины [math]v[/math] (англ. Arbitrarily traceable graph), если любая цепь с началом в вершине [math]v[/math] может быть продолжена до эйлерового цикла графа [math]G[/math]. Разумеется, если граф произвольно вычерчиваем из вершины [math]v[/math], то он является эйлеровым графом.

Теорема:

Неодноэлементный эйлеров граф [math]G[/math] является произвольно вычерчиваемым из вершины [math]v[/math] [math]\Longleftrightarrow[/math] вершина [math]v[/math] принадлежит всем циклам графа [math]G[/math].

Доказательство:

[math]\triangleright[/math]

[math]\Leftarrow[/math] Пусть вершина [math]v[/math] эйлерова графа [math]G[/math] принадлежит любому циклу. Рассмотрим произвольную [math](v, w)[/math]-цепь [math]P[/math] и покажем, что её можно продолжить до эйлерового цикла. Обозначим через [math]G_1[/math] подграф графа [math]G[/math], полученный удалением из [math]G[/math] всех рёбер цепи [math]P[/math]. Если [math]w=v[/math], то все вершины подграфа [math]G_1[/math] имеют чётную степень, если же [math]w\ne v[/math], то [math]G_1[/math] содержит в точности две вершины нечётной степени. Пусть [math]H_0[/math] — компонента связности графа [math]G_1[/math], содержащая вершину [math]v[/math]. Ясно, что вершина [math]w[/math] принадлежит [math]H_0[/math]. Следовательно, [math]H_0[/math] — полуэйлеров граф, и потому в [math]H_0[/math] существует эйлерова [math](v, w)[/math]-цепь [math]Q[/math]. [math]H_0[/math] содержит все рёбра графа [math]G_1[/math]. Предположим, что [math]G_1[/math] содержит неодноэлементную компоненту связности [math]H[/math], отличную от [math]H_0[/math]. Тогда [math]H[/math] — эйлеров граф, и потому в [math]H[/math] содержится цикл. Этот цикл не проходит через вершину [math]v[/math], что невозможно. Следовательно, все компоненты связности подграфа [math]G_1[/math], отличные от [math]H_0[/math], одноэлементны. Таким образом, цепь [math]Q[/math] содержит все рёбра графа [math]G_1[/math]. Отсюда вытекает, что объединение цепей [math]P[/math] и [math]Q[/math] — эйлеров цикл в графе [math]G[/math], являющийся продолжением цепи [math]P[/math]. [math]\Rightarrow[/math] Пусть в графе [math]G[/math] существует цикл [math]C[/math], не содержащий вершину [math]v[/math]. Рассмотрим подграф [math]G_1[/math], полученный удалением из [math]G[/math] всех рёбер цикла [math]C[/math]. Пусть [math]H[/math] — компонента связности подграфа [math]G_1[/math], содержащая вершину [math]v[/math]. Легко понять, что [math]H[/math] — эйлеров граф. Обозначим через [math]P[/math] эйлеров цикл подграфа. Можно считать, что началом и концом цикла [math]P[/math] является вершина [math]v[/math]. Поскольку [math]v[/math] не принадлежит циклу [math]C[/math], цепь [math]P[/math] нельзя продолжить до эйлерового цикла графа [math]G[/math].

[math]\triangleleft[/math]

Строение

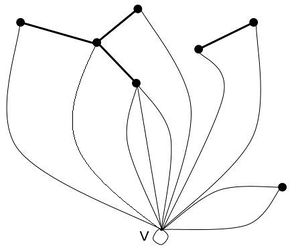
Опираясь на теорему несложно описать строение всех графов, произвольно вычерчиваемых из вершины [math]v[/math].
Возьмем произвольный лес [math]H[/math], не содержащий вершину [math]v[/math]. Каждую вершину нечетной степени соединим некоторым нечетным числом кратных ребер с [math]v[/math], а каждую вершину четной степени [math]--[/math] четным числом кратных ребер с [math]v[/math] (не исключая 0), причем каждую изолированную вершину обязательно соединим с [math]v[/math].
Полученный граф [math]G[/math]:

• Связен;
• Имеет только вершины четной степени;
• Является произвольно вычерчиваемым из [math]v[/math], как эйлеров граф, у которого [math]v[/math] принадлежит всем циклам.

Источники

Асанов М., Баранский В., Расин В. Дискретная математика: Графы, матроиды, алгоритмы. — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001. — С. 36. — ISBN 5-93972-076-5