Марковская цепь

Определение:

Цепь Маркова — процесс, находящийся в одном из [math]n[/math] состояний. При этом, если он находится в состоянии с номером [math]i[/math], то он перейдет в состояние [math]j[/math] с вероятностью [math]p_{ij}[/math]. Матрицу [math]P = ||p_{ij}||[/math] называют матрицей переходов.

Пример марковской цепи

На матрицу переходов накладываются следующие условия:

1. [math] p_{ij} \geqslant 0 [/math]
2. [math] \forall i\ \ \sum\limits_{j} p_{ij} = 1 [/math]

Такая матрица называется стохастической.

В общем случае для марковской цепи задают вектор [math] c_0[/math]. [math]\ c_{0i} [/math] — вероятность того, что в начале процесса марковская цепь находится в состоянии [math] i [/math].

Марковскую цепь можно представить в виде графа, в котором вершины — это состояния процесса, а ребра — переходы между состояниями, и на ребре из [math] i [/math] в [math] j [/math] написана вероятность перехода из [math] i [/math] в [math] j [/math], то есть [math] p_{ij} [/math].

Вероятность того, что через [math] r [/math] шагов марковская цепь будет находиться в состоянии [math] j [/math] равна [math] c_{rj} = (c_0 P^r) [j] [/math]

Классификация цепей и состояний

Определение:

[math] p_{ij}^{(n)} [/math] — вероятность попасть из состояния [math] i [/math] в состояние [math] j [/math] за [math] n [/math] переходов.

Определение:

Состояние [math] j [/math] достижимо (accesible) из состояния [math] i [/math], если существует такое [math] n [/math], что [math] p_{ij}^{(n)} \gt 0 [/math]. Достижимость [math] j [/math] из [math] i [/math] обозначается [math] i \rightarrow j [/math]. Состояния сообщаются (communicate), если они достижимы друг из друга.

Определение:

Неразложимый класс (communicating class) — класс эквивалентности множества состояний по отношению сообщаемости. Если представить Марковскую цепь как граф, неразложимый класс будет аналогичен компоненте сильной связности. Неразложимая цепь (ireducible chain) — цепь Маркова, в которой все состояния образуют один неразложимый класс.

Определение:

Упорядочим (очевидно, упорядочение будет частичным) неразложимые классы отношением достижимости. Минимальные элементы в таком упорядочении называются эргодическими классами. Состояния в эргодических классах называются эргодическими (ergodic), возвратными, или существенными. Если эргодический класс состоит из одного состояния, такое состояние называется поглощающим (absorbing). Из свойств частичного упорядочения, в любой цепи Маркова найдется хотя бы один эргодический класс. Все остальные неразложимые классы называются невозвратными классами. Состояния, входящие в них, называются невозвратными или несущественными.

Определение:

Поглощающей (absorbing chain) называется марковская цепь, в которой есть хотя бы одно поглощающее состояние и из любого состояния достижимо хотя бы одно поглощающее.

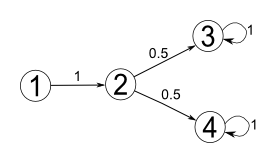
В примере на рисунке поглощающими являются состояния 3 и 4, а непоглощающими — 1 и 2.

Смотри также

• Теорема о поглощении

• Цепь Маркова
• Андрей Андреевич Марков

Литература

• И.В. Романовский. «Дискретный анализ»