Теорема Хватала — различия между версиями
| Строка 104: | Строка 104: | ||
<tex> S \cap T = \emptyset </tex>. | <tex> S \cap T = \emptyset </tex>. | ||
|proof= | |proof= | ||
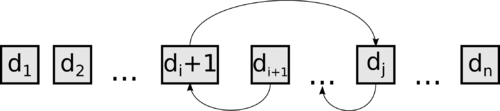
| − | Пусть <tex> j \in S \cap T </tex>. Тогда получим гамильтонов цикл графа <tex> G </tex>: <tex> u_1 \rightarrow^{e_j} u_{j + 1} \rightarrow u_{j + 2} \rightarrow \ldots \rightarrow u_n \rightarrow^{f_j} u_j \rightarrow u_{j - 1} \rightarrow \ldots \rightarrow u_1 </tex>, что противоречит условию, что граф негамильтонов. Значит, <tex> S \cap T </tex>, q.e.d. | + | Пусть <tex> j \in S \cap T </tex>. Тогда получим гамильтонов цикл графа <tex> G </tex>: <tex> u_1 \rightarrow^{e_j} u_{j + 1} \rightarrow u_{j + 2} \rightarrow \ldots \rightarrow u_n \rightarrow^{f_j} u_j \rightarrow u_{j - 1} \rightarrow \ldots \rightarrow u_1 </tex>, что противоречит условию, что граф негамильтонов. |
| + | [[Файл: Hvatal_4.png|400px|thumb|center|]] | ||
| + | Значит, <tex> S \cap T </tex>, q.e.d. | ||
}} | }} | ||
Версия 01:10, 27 февраля 2012
| Определение: |
| Пусть неориентированный граф имеет вершин: . Пусть и вершины графа упорядочены таким образом, что . Последовательность называют последовательностью степеней графа . |
| Лемма (О добавлении ребра в граф): |
Пусть неориентированный граф получен из неориентированного графа добавлением одного нового ребра . Тогда последовательность степеней графа мажорируется последовательностью степеней графа . |
| Доказательство: |
|
Замечание: Если в неубывающей последовательности увеличить на единицу число , а затем привести последовательность к неубывающему виду, переставив число на положенное место , то исходная последовательность будет мажорироваться полученной. Если , то утверждение леммы, очевидно, выполняется. Пусть .
При добавлении в граф ребра , степени вершин и увеличатся на единицу. Для доказательства леммы, дважды воспользуемся замечанием. Значит, последовательность степеней полученного графа мажорирует последовательность степеней исходного, q.e.d. |
| Теорема (Хватал): | |||||||||||||||||||||||
Пусть:
Тогда если верна импликация: | |||||||||||||||||||||||
| Доказательство: | |||||||||||||||||||||||
|
Для доказательства теоремы, докажем 3 леммы.
Приведем доказательство от противного. Пусть существует граф с числом вершин , удовлетворяющий , но негамильтонов. Будем добавлять в него ребра до тех пор, пока не получим максимально возможный негамильтонов граф (то есть добавление еще одного ребра сделает граф гамильтоновым). По лемме о добавлении ребра и лемме №3 импликация остается верной для графа . Очевидно, что граф гамильтонов при . Будем считать максимальным негамильтоновым остовным подграфом графа . Выберем две несмежные вершины и графа , такие что — максимально. Будем считать, что . Добавив к новое ребро , получим гамильтонов граф . Рассмотрим гамильтонов цикл графа : в нём обязательно присутствует ребро . Отбрасывая ребро , получим гамильтонову -цепь в графе : . Пусть .
Из определений и следует, что . Значит, . Так как , ни одна вершина не смежна с (для ). В силу выбора и , получим, что . Пусть . Значит, вершин, степень которых не превосходит . По лемме №1: . В силу импликации : . По лемме №2, вершин, степень которых не меньше . Так как , то вершина может быть смежна максимум с из этих вершин. Значит, существует вершина , не являющаяся смежной с и для которой . Тогда получим, что , что противоречит выбору и . Значит, предположение неверно, q.e.d. | |||||||||||||||||||||||
См. также
Литература
- Асанов М., Баранский В., Расин В.: Дискретная математика: Графы, матроиды, алгоритмы