Персистентный дек — различия между версиями
Shersh (обсуждение | вклад) |
Shersh (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
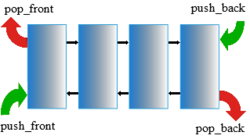
'''Дек''' (англ. deque {{---}} double ended queue {{---}} очередь с двумя концами) {{---}} структура данных с двусторонним доступом к элементам, т. е. их можно удалять и добавлять как в начало, так и в конец дека. | '''Дек''' (англ. deque {{---}} double ended queue {{---}} очередь с двумя концами) {{---}} структура данных с двусторонним доступом к элементам, т. е. их можно удалять и добавлять как в начало, так и в конец дека. | ||
}} | }} | ||
| − | [[Файл:Deque.png|thumb| | + | [[Файл:Deque.png|thumb|250px|Дек]] |
| − | Кроме дека ещё существует структура данных, называемая ''steque'', которая представляет собой объединение стека и очереди - элементы можно добавлять только в один конец, а извлекать можно с обоих | + | Кроме дека ещё существует структура данных, называемая ''steque'', которая представляет собой объединение стека и очереди - элементы можно добавлять только в один конец, а извлекать можно с обоих. |
== Эффективная реализация == | == Эффективная реализация == | ||
Написать дек на массиве не представляет особого труда, зная уже, как работают стек и очередь. Далее будет приведена реализация операций добавление элемента и извлечение из одного конца дека за истинное время работы <tex> O(\log ~ n). </tex> Добавление и исключение из другого конца делается симметрично. | Написать дек на массиве не представляет особого труда, зная уже, как работают стек и очередь. Далее будет приведена реализация операций добавление элемента и извлечение из одного конца дека за истинное время работы <tex> O(\log ~ n). </tex> Добавление и исключение из другого конца делается симметрично. | ||
| + | [[Файл:Tree_deque.png|thumb|Древовидная структура дека]] | ||
| + | |||
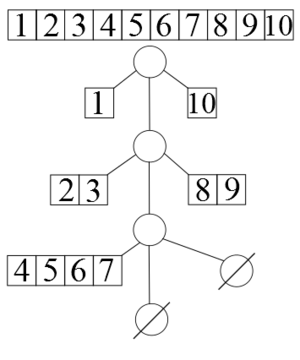
| + | Персистентный дек можно визуально представить как дерево, где каждый узел хранит пару первый элемент и последний, а также ''ребёнка'' - ссылку на следующий дек. Только с каждым уровнем вложенности левый и правый элемент представляют собой массив размера в два раза больше, чем на предыдущем уровне. | ||
<code> | <code> | ||
Версия 18:03, 9 марта 2012
| Определение: |
| Дек (англ. deque — double ended queue — очередь с двумя концами) — структура данных с двусторонним доступом к элементам, т. е. их можно удалять и добавлять как в начало, так и в конец дека. |
Кроме дека ещё существует структура данных, называемая steque, которая представляет собой объединение стека и очереди - элементы можно добавлять только в один конец, а извлекать можно с обоих.
Эффективная реализация
Написать дек на массиве не представляет особого труда, зная уже, как работают стек и очередь. Далее будет приведена реализация операций добавление элемента и извлечение из одного конца дека за истинное время работы Добавление и исключение из другого конца делается симметрично.
Персистентный дек можно визуально представить как дерево, где каждый узел хранит пару первый элемент и последний, а также ребёнка - ссылку на следующий дек. Только с каждым уровнем вложенности левый и правый элемент представляют собой массив размера в два раза больше, чем на предыдущем уровне.
Deque<T>(first, child, last)
Deque<T> {
T first, last;
Deque<T> child;
};
Так как наша структура данных персистентная, то операция возвращает новый дек , c элементом в начале.
push_front(x) if first == return Deque<T>(x, child, last) else return Deque<T>(, c.push_front(Pair<x, first>), last)
Метод возвращает пару из первого элемента и нового дека, полученного из старого изъятием этого элемента.
pop_front() if first return first, Deque<T>(, child, last) else if child == return last, Deque<T>() else temp, newDeque child.pop_front() if temp == return last, Deque<T>() else return temp.first, Deque<T>(temp.child, newDeque, last)
Чтобы извлечь элемент, придётся спуститься не больше, чем на глубину дерева. Аналогично для добавления. Поэтому обе операции выполняются за