Раскраска графа

Раскраска графа

Определение:

Правильной раскраской графа [math]G(V,E)[/math] называется такое отображение [math]\phi[/math] из множества вершин [math]V[/math] в множество красок [math]\{c_1...c_t\}[/math], что для любых двух смежных вершин [math]u[/math] и [math]v[/math] выполняется [math]\phi(u)\ne\phi(v)[/math]. Так же её называют [math]t[/math]-раскраской.

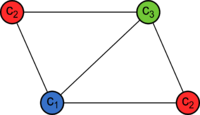
Раскраской графа чаще всего называют именно правильную раскраску.

Хроматическое число

Определение:

Хроматическим числом [math]\chi(G)[/math] графа [math]G(V,E)[/math] называется такое минимальное число [math]t[/math], для которого существует [math]t[/math]-раскраска графа.

Хроматические числа различных графов

1) [math]1[/math]-хроматические графы - это нулевые графы и только они. [math]\chi(O_{n}) = 1[/math].

2) [math]\chi(K_{n}) = n[/math] — хроматическое число полного графа равно [math]n[/math].

3) [math]\chi(C_{n}) = \begin{cases} 2\text{, if $n$ is even;}\\ 3\text{, if $n$ is odd.} \end{cases} [/math]

4) [math]G[/math] - дерево, тогда [math]\chi(G) = 2[/math]

Задача о нахождении [math]\chi(G)[/math] не разрешима за полиномиальное время.

Хроматический многочлен

Определение:

Хроматическим многочлен [math]P(G, t)[/math] — число способов раскрасить граф [math]G[/math] в [math]t[/math] цветов.

Источники

1. Асанов М. О., Баранский В. А., Расин В. В. - Дискретная математика: Графы, матроиды, алгоритмы. ISBN 978-5-8114-1068-2
2. Харари Ф. - Теория графов. ISBN 978-5-397-00622-4