Splay-дерево

Сплей-дерево (Splay-tree) — это двоичное дерево поиска. Оно позволяет находить быстрее те данные, которые использовались недавно. Относится к разряду сливаемых деревьев. Сплей-дерево было придумано Робертом Тарьяном и Даниелем Слейтером в 1983 году.

Эвристики

Для того, чтобы доступ к недавно найденным данным был быстрее, надо, чтобы эти данные находились ближе к корню. Этого мы можем добиться, используя различные эвристики:

• Move to Root — совершает повороты вокруг ребра [math](x, p)[/math], где [math]x[/math] - найденная вершина, [math]p[/math] - ее предок, пока [math]x[/math] не окажется корнем дерева. Однако можно построить такую последовательность операций, что амортизированное время доступа к вершине будет [math] O(n) [/math].
• Splay — также совершает повороты, но чередует различные виды поворотов, благодаря чему достигается логарифмическая амортизированная оценка. Она будет подробно описана ниже.

Операции со splay-деревом

Splay(Tree, x)

"Splay" делится на 3 случая:

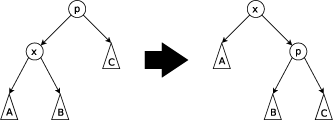
Zig

Если [math]p[/math] - корень дерева с сыном [math]x[/math], то совершаем один поворот вокруг ребра [math](x, p)[/math], делая [math]x[/math] корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина [math]x[/math] была нечетной.

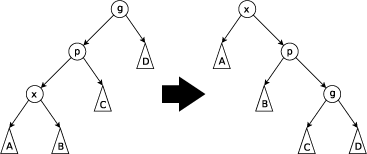
Zig-Zig

Если [math]p[/math] - не корень дерева, а [math]x[/math] и [math]p[/math] - оба левые или оба правые дети, то делаем поворот ребра [math](p, g)[/math], где [math]g[/math] отец [math]p[/math], а затем поворот ребра [math](x, p)[/math].

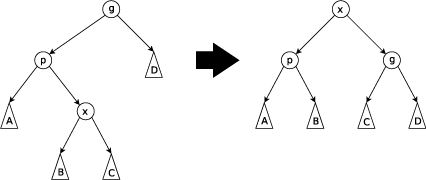
Zig-Zag

Если [math]p[/math] - не корень дерева и [math]x[/math] - левый ребенок, а [math]p[/math] - правый, или наоборот, то делаем поворот вокруг ребра [math](x, p)[/math], а затем поворот нового ребра [math](x, g)[/math], где [math]g[/math] - бывший родитель [math]p[/math].

Данная операция занимает [math]O(d)[/math] времени, где [math]d[/math] - длина пути от [math]x[/math] до корня. В результате этой операции [math]x[/math] становится корнем дерева, а расстояние до корня от каждой вершины сокращается примерно пополам, что связано с разделением случаев "zig-zig" и "zig-zag".

Find(Tree, x)

Эта операция выполняется как для обычного бинарного дерева , только после нее запускается операция Splay.

Merge(Tree1, Tree2)

У нас есть два дерева [math]Tree1[/math] и [math]Tree2[/math], причём подразумевается, что все элементы первого дерева меньше элементов второго. Запускаем Splay от самого большого элемента в дереве [math]Tree1[/math] (пусть это элемент [math]i[/math]). После этого корень [math]Tree1[/math] содержит элемент [math]i[/math], при этом у него нет правого ребёнка. Делаем [math]Tree2[/math] правым поддеревом [math]i[/math] и возвращаем полученное дерево.

Split(Tree, x)

Запускаем Splay от элемента [math]x[/math] и возвращаем два дерева, полученные отсечением правого или левого поддерева от корня, в зависимости от того, содержит корень элемент больше или не больше, чем [math]x[/math].

Add(Tree, x)

Запускаем Split(Tree, x), который нам возвращает деревья [math]Tree1[/math] и [math]Tree2[/math], их подвешиваем к [math]x[/math] как левое и правое поддеревья соответственно.

Remove(Tree, x)

Запускаем Splay от [math]x[/math] элемента и возвращаем Merge от его детей.

Анализ операции splay

Амортизационный анализ сплей-дерева проводится с помощью метода потенциалов. Потенциалом рассматриваемого дерева назовём сумму рангов его вершин. Ранг вершины [math]x[/math] — это величина, обозначаемая [math]r(x)[/math] и равная [math]\log_2 C(x)[/math], где [math]C(x)[/math] — количество вершин в поддереве с корнем в [math]x[/math].

Лемма:

Амортизированное время операции splay вершины [math]x[/math] в дереве с корнем [math]t[/math] не превосходит [math]3r(t) - 3r(x) + 1[/math]

Доказательство:

[math]\triangleright[/math]

Проанализируем каждый шаг операции splay. Пусть [math]r'[/math] и [math]r[/math] — ранги вершин после шага и до него соответственно, [math]p[/math] — предок вершины [math]x[/math], а [math]g[/math] — предок [math]p[/math] (если есть). Разберём случаи в зависимости от типа шага: Zig. Поскольку выполнен один поворот, то время амортизированное время выполнения шага [math]T = 1 + r'(x) + r'(p) - r(x) - r(p)[/math] (поскольку только у вершин [math]x[/math] и [math]p[/math] меняется ранг). Ранг вершины [math]p[/math] уменьшился, поэтому [math]T \le 1 + r'(x) - r(x)[/math]. Ранг вершины [math]x[/math] увеличился, поэтому [math]r'(x) - r(x) \ge 0[/math]. Следовательно, [math]T \le 1 + 3r'(x) - 3r(x)[/math]. Zig-zig. Выполнено два поворота, амортизированное время выполнения шага [math]T = 2 + r'(x) + r'(p) + r'(g) - r(p) - r(x) - r(g)[/math]. Поскольку после поворотов поддерево с корнем в [math]x[/math] будет содержать все вершины, которые были в поддереве с корнем в [math]g[/math] (и только их), поэтому [math]r'(x) = r(g)[/math]. Используя это равенство, получаем: [math]T = 2 + r'(p) + r'(g) - r(x) - r(p) \le 2 + r'(p) + r'(g) - 2r(x)[/math], поскольку [math]r(x) \le r(p)[/math]. Далее, так как [math]r'(p) \le r'(x)[/math], получаем, что [math]T \le 2 + r'(x) + r'(g) - 2r(x)[/math]. Мы утверждаем, что эта сумма не превосходит [math]3(r'(x) - r(x))[/math], то есть, что [math]r(x) + r'(g) - 2r'(x) \le -2[/math]. Преобразуем полученное выражение следующим образом: [math](r(x) - r'(x)) + (r'(g) - r'(x)) = \log_2 \frac{C(x)}{C'(x)} + \log_2 \frac{C'(g)}{C'(x)}[/math]. Из рисунка видно, что [math]C'(g) + C(x) \le C'(x)[/math], значит, сумма выражений под логарифмами не превосходит единицы. Далее, рассмотрим сумму логарифмов [math]\log_2 a + \log_2 b = \log_2 ab[/math]. При [math]a + b \le 1[/math] произведение [math]ab[/math] по неравенству между средними не превышает [math]1/4[/math]. А поскольку логарифм - функция возрастающая, то [math]\log_2 ab \le -2[/math], что и является требуемым неравенством. Zig-zag. Выполнено два поворота, амортизированное время выполнения шага [math]T = 2 + r'(x) + r'(p) + r'(g) - r(x) - r(p) - r(g)[/math]. Поскольку [math]r'(x) = r(g)[/math], то [math]T = 2 + r'(p) + r'(g) - r(x) - r(p)[/math]. Далее, так как [math]r(x) \le r(p)[/math], то [math]T \le 2 + r'(p) + r'(g) - 2r(x)[/math]. Мы утверждаем, что эта сумма не превосходит [math]2(r'(x) - r(x))[/math], то есть, что [math]r'(p) + r'(g) - 2r'(x) \le -2[/math]. Но, поскольку [math]r'(p) + r'(g) - 2r'(x) = \log_2 \frac{C'(p)}{C'(x)} + \log_2 \frac{C'(g)}{C'(x)} \le -2[/math] - аналогично доказанному ранее, что и требовалось доказать. Итого, получаем, что амортизированное время шага zig-zag не превосходит [math]2(r'(x) - r(x)) \le 3(r'(x) - r(x))[/math]. Поскольку за время выполнения операции splay выполняется не более одного шага типа zig, то суммарное время не будет превосходить [math]3r(t) - 3r(x) + 1[/math], поскольку утроенные ранги промежуточных вершин сокращаются (входят в сумму как с плюсом, так и с минусом).

[math]\triangleleft[/math]

Splay-деревья по неявному ключу

Для операции split нам необходимо хранить число вершин в поддереве. Это число может меняться вовремя операции splay, но при этом его легко поддерживать: мы точно знаем, куда переместятся поддеревья. Тогда после операции мы просто пересчитываем число элементов для 2 (zig) или 3 (zig-zig, zig-zag) вершин. Остальные операции аналогичны декартову дереву по неявному ключу.

Литература

• Википедия - Splay tree
• Sleator, Daniel D.; Tarjan, Robert E."Self-Adjusting Binary Search Trees"