Ортогональный поиск — различия между версиями
Proshev (обсуждение | вклад) |
|||
| Строка 1: | Строка 1: | ||
== Простейший случай == | == Простейший случай == | ||
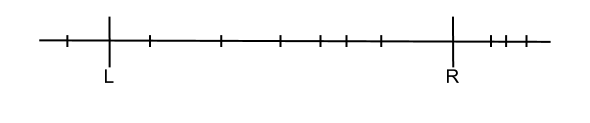
| − | Пусть дана прямая с точками на ней и отрезок. Необходимо указать, какие из изначальных точек лежат на этом отрезке. | + | Пусть дана прямая с точками на ней и отрезок. Точки даны в отсортированном порядке. Необходимо указать, какие из изначальных точек лежат на этом отрезке. |
| − | Данная задача решается с помощью функций из STL - upper_bound и lower_bound | + | [[Файл:Line_with_dots_and_segment.png]] |
| + | |||
| + | Данная задача решается с помощью функций из STL - upper_bound и lower_bound. | ||
| + | |||
| + | upper_bound возвращает наименьшее значение больше данного, lower_bound - наибольшее значение меньше данного. | ||
| + | |||
| + | Рассмотрим на примере: | ||
| + | |||
| + | [[Файл:Upper_bound_and_lower_bound.png]] | ||
Код реализации: | Код реализации: | ||
| Строка 13: | Строка 21: | ||
== Сбалансированное дерево поиска == | == Сбалансированное дерево поиска == | ||
| + | |||
| + | Переходим к двумерному случаю. Пусть дано некоторое множество точек на плоскости. Нам необходимо ответить, какие именно из них лежат в некотором заданном прямоугольнике. | ||
| + | |||
| + | Для этого возьмем любое сбалансированное дерево поиска и слегка модернизируем его для более быстрой работы. | ||
| + | |||
| + | В каждом узле будем хранить точки, которые входят в его поддерево. | ||
| + | |||
| + | Теперь для ответа нам нужно спуститься отрезком по дереву и, если все поддерево лежит в отрезке, сразу выдавать его, если нет - спускаться дальше. | ||
== Квадро дерево == | == Квадро дерево == | ||
== Инкрементальное квадро дерево == | == Инкрементальное квадро дерево == | ||
Версия 10:13, 25 апреля 2012
Содержание
Простейший случай
Пусть дана прямая с точками на ней и отрезок. Точки даны в отсортированном порядке. Необходимо указать, какие из изначальных точек лежат на этом отрезке.
Данная задача решается с помощью функций из STL - upper_bound и lower_bound.
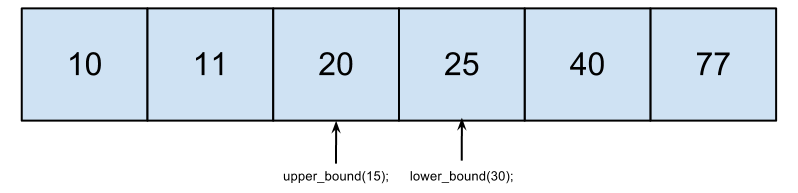
upper_bound возвращает наименьшее значение больше данного, lower_bound - наибольшее значение меньше данного.
Рассмотрим на примере:
Код реализации:
template<class RauIter, class OutIter, class Scalar> OutIter range_search(RauIter p, RauIter q, OutIter out)
{
return std::copy(lower_bound(p, q, l), upper_bound(p, q, r), out);
}
Сбалансированное дерево поиска
Переходим к двумерному случаю. Пусть дано некоторое множество точек на плоскости. Нам необходимо ответить, какие именно из них лежат в некотором заданном прямоугольнике.
Для этого возьмем любое сбалансированное дерево поиска и слегка модернизируем его для более быстрой работы.
В каждом узле будем хранить точки, которые входят в его поддерево.
Теперь для ответа нам нужно спуститься отрезком по дереву и, если все поддерево лежит в отрезке, сразу выдавать его, если нет - спускаться дальше.