Реализация запроса в дереве отрезков снизу — различия между версиями
Lirik (обсуждение | вклад) |
Lirik (обсуждение | вклад) |
||
| Строка 9: | Строка 9: | ||
==Псевдокод== | ==Псевдокод== | ||
| − | Пусть ассоциативная операция | + | Пусть ассоциативная операция, над которой построено дерево отрезков, обозначается a <tex> \circ </tex> b, а результат считаем на отрезке [left, right]. |
| − | + | query(left, right) | |
| − | result = | + | result = neutral; //Присваиваем результату значение нейтральное элемента(например для поиска суммы надо присвоить значение 0) |
while left < right //Выполняем цикл до тех пор, пока левая и правая граница не пересекутся | while left < right //Выполняем цикл до тех пор, пока левая и правая граница не пересекутся | ||
if (left div 2) * 2 == left // Проверяем, является ли левая граница правым сыном (индексация с 0) | if (left div 2) * 2 == left // Проверяем, является ли левая граница правым сыном (индексация с 0) | ||
| − | result = | + | result = result <tex> \circ </tex> data[left]; // Если является, то пересчитаем результат и перенесем левую границу |
left = (left + 1) div 2; | left = (left + 1) div 2; | ||
else | else | ||
left = left div 2; // Если не является, то установим границу на родительский элемент текущей границы | left = left div 2; // Если не является, то установим границу на родительский элемент текущей границы | ||
if (right div 2) * 2 + 1 == right // Аналогично проделываем операции с правой границей | if (right div 2) * 2 + 1 == right // Аналогично проделываем операции с правой границей | ||
| − | result = | + | result = result <tex> \circ </tex> data[right]; |
right = (right - 1) div 2; | right = (right - 1) div 2; | ||
else | else | ||
right = right div 2; | right = right div 2; | ||
if left == right // После окончания цикла проверяем совпали ли границы | if left == right // После окончания цикла проверяем совпали ли границы | ||
| − | result = | + | result = result <tex> \circ </tex> data[left]; // Если надо пересчитываем результат |
return result; | return result; | ||
Версия 18:36, 26 мая 2012
Алгоритм
Реализация запроса снизу вверх в дереве отрезков является, в отличие от реализации запроса сверху вниз, итеративным методом. Будем рассматривать абстрактную операцию, обладающую свойством ассоциативности.
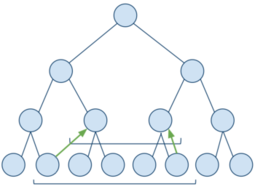
Построим дерево отрезков и установим границы отрезка на соответствующие листья. Если элемент, попавший на левую границу, является правым сыном, то запишем в результат значение, полученное после выполнения нашей операции над предыдущим результатом и значением этого элемента, а левую границу перемещаем на один элемент вправо. Аналогично действуем с элементом попавшим на правую границу (является ли этот элемент левым сыном). Затем устанавливаем границы отрезка на родительские элементы текущих границ. Продолжаем до тех пор, пока границы не пересекутся.
Псевдокод
Пусть ассоциативная операция, над которой построено дерево отрезков, обозначается a b, а результат считаем на отрезке [left, right].
query(left, right)
result = neutral; //Присваиваем результату значение нейтральное элемента(например для поиска суммы надо присвоить значение 0)
while left < right //Выполняем цикл до тех пор, пока левая и правая граница не пересекутся
if (left div 2) * 2 == left // Проверяем, является ли левая граница правым сыном (индексация с 0)
result = result data[left]; // Если является, то пересчитаем результат и перенесем левую границу
left = (left + 1) div 2;
else
left = left div 2; // Если не является, то установим границу на родительский элемент текущей границы
if (right div 2) * 2 + 1 == right // Аналогично проделываем операции с правой границей
result = result data[right];
right = (right - 1) div 2;
else
right = right div 2;
if left == right // После окончания цикла проверяем совпали ли границы
result = result data[left]; // Если надо пересчитываем результат
return result;