Сведение задачи LCA к задаче RMQ — различия между версиями
| Строка 24: | Строка 24: | ||
Приведенный выше алгоритм работает верно. | Приведенный выше алгоритм работает верно. | ||
|proof= | |proof= | ||
| − | Рассмотрим два узла <tex>u, v</tex> корневого дерева <tex>T</tex>. Для определенности считаем, что <tex>u</tex> является первой при поиске в глубину | + | Рассмотрим два узла <tex>u, v</tex> корневого дерева <tex>T</tex>. Для определенности считаем, что <tex>u</tex> является первой при поиске в глубину. Рассмотрим отрезок <tex>depth[I[u]..I[v]]</tex>. Поскольку этот отрезок {{---}} путь из <tex>u</tex> в <tex>v</tex>, он проходит через их наименьшего общего предка <tex>w</tex>(в дереве есть только один простой путь между вершинами). Покажем, что его глубина минимальна на отрезке <tex>depth[I[u]..I[v]]</tex>. Допустим обратное. Все потомки <tex>w</tex> имеют глубину больше. Но тогда получим, что поиск в глубину вышел из поддерева вершины <tex>w</tex> раньше, чем посетил вершину <tex>v</tex>. |
}} | }} | ||
Версия 00:06, 31 мая 2012
Содержание
Постановка задачи LCA
| Определение: |
| Наименьшим общим предком (least common ancestor) двух узлов в корневом дереве называется узел который среди всех узлов, являющихся предками как узла так и имеет наибольшую глубину. |
Пусть дано корневое дерево На вход подаются запросы вида для каждого запроса требуется найти их наименьшего общего предка.
Алгоритм
Препроцессинг
1) В каждом узле будет храниться глубина узла в корневом дереве
2) Запустим обход в глубину из корня, который будет строить список посещений узлов. Глубина текущей вершины добавляется в список при входе в эту вершину, а также после каждого возвращения из её сына.
Запрос
Обозначим — функция, возвращающая любой индекс ячейки в списке глубин , в котором хранится глубина узла . Ее можно строить во время обхода в глубину. Пусть имеется запрос пара узлов В результате обхода в глубину получился список глубин вершин, в котором наименьшему общему предку вершин соответствует минимальная глубина на отрезке Для определённости
Доказательство корректности алгоритма
| Теорема: |
Приведенный выше алгоритм работает верно. |
| Доказательство: |
| Рассмотрим два узла корневого дерева . Для определенности считаем, что является первой при поиске в глубину. Рассмотрим отрезок . Поскольку этот отрезок — путь из в , он проходит через их наименьшего общего предка (в дереве есть только один простой путь между вершинами). Покажем, что его глубина минимальна на отрезке . Допустим обратное. Все потомки имеют глубину больше. Но тогда получим, что поиск в глубину вышел из поддерева вершины раньше, чем посетил вершину . |
Пример
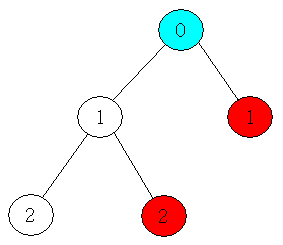
Рассмотрим дерево на рисунке 1. Найдем наименьшего общего предка вершин, помеченных красным цветом. Список глубин, получающийся в результате обхода в глубину - Глубина наименьшего общего предка красных вершин равна минимуму на отрезке
Сложность
Для нахождения минимального элемента на отрезке можно использовать дерево отрезков. Длина массива глубин будет равна т.е. дерево отрезков будет построено за Таким образом, препроцессинг работает за Время выполнения запроса равно времени запроса минимального элемента на отрезке в дереве отрезков, т.е.
См.также
- Метод двоичного подъема
- Решение RMQ с помощью разреженной таблицы
- Алгоритм Фарака-Колтона и Бендера
- Сведение задачи RMQ к задаче LCA