Карманная сортировка — различия между версиями
Daniel (обсуждение | вклад) |
Daniel (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | '''Карманная сортировка'''(Bucket sort) — алгоритм сортировки , основанный на предположении о равномерном распределении входных данных. | + | '''Карманная сортировка''' (Bucket sort) — алгоритм сортировки , основанный на предположении о равномерном распределении входных данных. |
== Алгоритм сортировки == | == Алгоритм сортировки == | ||
=== Принцип работы === | === Принцип работы === | ||
| Строка 7: | Строка 7: | ||
* каждый из блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения. | * каждый из блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения. | ||
* из каждого отсортированного блока данные записываются в массив в порядке разбиения на блоки. | * из каждого отсортированного блока данные записываются в массив в порядке разбиения на блоки. | ||
| − | Важно отметить ,что разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были бы больше предыдущего. | + | Важно отметить, что разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были бы больше предыдущего. |
=== Реализация === | === Реализация === | ||
Рассмотрим код работы алгоритма, где <tex> p </tex> — длина каждой строки. | Рассмотрим код работы алгоритма, где <tex> p </tex> — длина каждой строки. | ||
<wikitex> | <wikitex> | ||
| − | Bucketsort(A, j){ // A - массив данных, j - текущий разряд | + | Bucketsort (A, j){ // A - массив данных, j - текущий разряд |
| − | if (A.length | + | if (A.length < 2 || j == p + 1) |
return A; | return A; | ||
buckets <- инициализируем массив длины Base, где каждая ячейка — список входных объектов (в нашем случае | buckets <- инициализируем массив длины Base, где каждая ячейка — список входных объектов (в нашем случае | ||
строк). | строк). | ||
| − | for i = 0 to A.length | + | for i = 0 to A.length - 1 |
| − | добавляем A[i] в конец массива buckets[partition(A[i],j)] | + | добавляем A[i] в конец массива buckets[partition (A[i], j)] |
// partition — функция которая по данному объекту и индексу возвращает число от 0 до Base - 1 | // partition — функция которая по данному объекту и индексу возвращает число от 0 до Base - 1 | ||
// в случае со строками функция partition возвращает код j-ого символа строки A[i]. | // в случае со строками функция partition возвращает код j-ого символа строки A[i]. | ||
for i = 0 to Base - 1 | for i = 0 to Base - 1 | ||
| − | buckets[i] = Bucketsort(buckets[i],j+1) | + | buckets[i] = Bucketsort (buckets[i],j+1) |
answer <- инициализируем пустой массив (в который записывается отсортированный набор данных) | answer <- инициализируем пустой массив (в который записывается отсортированный набор данных) | ||
for i = 0 to Base - 1 | for i = 0 to Base - 1 | ||
| − | for k = 0 to buckets[i].length | + | for k = 0 to buckets[i].length - 1 |
добавляем buckets[i][k] в конец массива answer | добавляем buckets[i][k] в конец массива answer | ||
return answer | return answer | ||
| Строка 33: | Строка 33: | ||
Приведенный код работает не только для строк, а для любых объектов для которых можно определить порядок, систему счисления и функцию partition. | Приведенный код работает не только для строк, а для любых объектов для которых можно определить порядок, систему счисления и функцию partition. | ||
==Асимптотика== | ==Асимптотика== | ||
| − | Пусть <tex>n</tex> | + | Пусть <tex>n</tex> - количество элементов в массиве, <tex>k</tex> - основание системы исчисления и |
| − | <tex>p</tex> | + | <tex>p</tex> - количество разрядов в объекте. |
| − | Тогда алгоритм "Bucket sort" в процессе работы сделает не более чем <Tex>O(p | + | Тогда алгоритм "Bucket sort" в процессе работы сделает не более чем <Tex>O (p \cdot (n + k))</Tex> итераций. |
| − | Заметим ,что в случае случайного распределения мат. ожидания количество элементов в каждом блоке <tex> n/k</tex>. Следовательно, в средним алгоритм "карманной сортировки" совершает <Tex>O(n \cdot log_k n)</Tex> действий. При этом на некотором множестве наборов, где <tex> k = O(n)</tex>, алгоритм отработает за линейное время. | + | Заметим, что в случае случайного распределения мат. ожидания количество элементов в каждом блоке <tex> n/k</tex>. Следовательно, в средним алгоритм "карманной сортировки" совершает <Tex>O (n \cdot log_k n)</Tex> действий. При этом на некотором множестве наборов, где <tex> k = O(n)</tex>, алгоритм отработает за линейное время. |
| − | В худшем случае сортировка работает за <tex>O(n^2)</tex>. | + | В худшем случае сортировка работает за <tex>O (n^2)</tex>. |
==Примечания== | ==Примечания== | ||
Сортировка быстро работает для равновероятного распределения значений разрядов объектов в заданной для них системе счисления. | Сортировка быстро работает для равновероятного распределения значений разрядов объектов в заданной для них системе счисления. | ||
Версия 19:51, 10 июня 2012
Карманная сортировка (Bucket sort) — алгоритм сортировки , основанный на предположении о равномерном распределении входных данных.
Содержание
Алгоритм сортировки
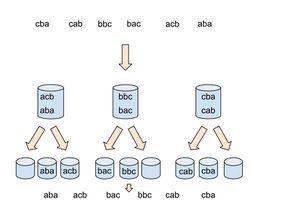
Принцип работы
- элементы массива входных данных разбиваются на блоков ("карманов","корзин").
- каждый из блоков сортируется либо другой сортировкой, либо рекурсивно тем же методом разбиения.
- из каждого отсортированного блока данные записываются в массив в порядке разбиения на блоки.
Важно отметить, что разбиение на блоки производится таким образом, чтобы элементы каждого следующего блока были бы больше предыдущего.
Реализация
Рассмотрим код работы алгоритма, где — длина каждой строки. <wikitex>
Bucketsort (A, j){ // A - массив данных, j - текущий разряд
if (A.length < 2 || j == p + 1)
return A;
buckets <- инициализируем массив длины Base, где каждая ячейка — список входных объектов (в нашем случае
строк).
for i = 0 to A.length - 1
добавляем A[i] в конец массива buckets[partition (A[i], j)]
// partition — функция которая по данному объекту и индексу возвращает число от 0 до Base - 1
// в случае со строками функция partition возвращает код j-ого символа строки A[i].
for i = 0 to Base - 1
buckets[i] = Bucketsort (buckets[i],j+1)
answer <- инициализируем пустой массив (в который записывается отсортированный набор данных)
for i = 0 to Base - 1
for k = 0 to buckets[i].length - 1
добавляем buckets[i][k] в конец массива answer
return answer
}
</wikitex> Base - основание системы счисления в случае со строками Base = 256.
Приведенный код работает не только для строк, а для любых объектов для которых можно определить порядок, систему счисления и функцию partition.
Асимптотика
Пусть - количество элементов в массиве, - основание системы исчисления и - количество разрядов в объекте. Тогда алгоритм "Bucket sort" в процессе работы сделает не более чем итераций. Заметим, что в случае случайного распределения мат. ожидания количество элементов в каждом блоке . Следовательно, в средним алгоритм "карманной сортировки" совершает действий. При этом на некотором множестве наборов, где , алгоритм отработает за линейное время. В худшем случае сортировка работает за .
Примечания
Сортировка быстро работает для равновероятного распределения значений разрядов объектов в заданной для них системе счисления. Быстрая сортировка является частным случаем "карманной" сортировки, в случае разбиения всех элементов на "кармана". Также стоит отметить, что по принципу своей работы Bucket sort схожа с Цифровой сортировкой.