Задача о наибольшей подпоследовательности-палиндроме — различия между версиями
(→Решение) |
(→Псевдокод) |
||
| Строка 36: | Строка 36: | ||
Если же в задаче необходимо вывести не длину, а саму подпоследовательность-палиндром, то дополнительно к массиву длин мы должны построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован. | Если же в задаче необходимо вывести не длину, а саму подпоследовательность-палиндром, то дополнительно к массиву длин мы должны построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован. | ||
| − | == | + | Размещаем граничные случаи: <tex>F(I, I) = 1</tex> и <tex>F(I, J) = 0</tex>, если <tex>I > J</tex>. Теперь в рассматриваемой подстроке отделяем первый символ. Есть две возможности (какая из них реализуется, пока не знаем). Отделенный символ не участвует в образовании максимального подпоследовательности-палиндрома — тогда <tex>F(I, J) = F(I + 1, J)</tex>. Если же участвует, то ищем в подстроке с конца символ, совпадающий с отделенным (пусть его позиция <tex>K</tex>), тогда <tex>F(I, J) = 2 + F(I + 1, K – 1)</tex>. Надо предусмотреть еще случай <tex>I = K</tex>, а затем отсекать рекурсию. |
| − | + | Получается следующая функция: | |
| + | Function F(i, j) | ||
| + | if L[i, j] == -1 | ||
| + | k = j | ||
| + | while S[i] <> S[k] | ||
| + | k-- | ||
| + | R1 = F(i + 1, j) | ||
| + | if i <> k | ||
| + | R2 = F(i + 1, k - 1) + 2 | ||
| + | else | ||
| + | R2 = 1 | ||
| + | if R1 > R2 | ||
| + | L[i, j] = R1 | ||
| + | else | ||
| + | L[i, j] = R2 | ||
| + | return L[i, j] | ||
== Литература == | == Литература == | ||
Версия 21:45, 13 декабря 2012
Задача о наибольшей подпоследовательности-палиндрома — это задача поиска длины наибольшей подпоследовательности-палиндрома, которую можно получить вычеркиванием некоторых букв из данной последовательности.
Содержание
Определения
| Определение: |
| Палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево. |
| Определение: |
| Подпоследовательностью-палиндромом данной строки называется последовательность символов из данной строки, не обязательно идущих подряд, являющаяся палиндромом. |
Например, HELOLEH является подпоследовательностью-палиндромом строки HTEOLFEOLEH.
Решение
Обозначим данную последовательность через , а ее элементы — через Будем рассматривать возможные подпоследовательности данной последовательности с го по ый символ, обозначим их как . Длины максимальных палиндромов для подпоследовательностей будем записывать в квадратный массив : — длина максимальной подпоследовательности-палиндрома, который можно получить из подпоследовательности .
Начнем решать задачу с простых подпоследовательностей. Для последовательности из одного элемента (то есть подпоследовательности вида ) ответ очевиден — ничего вычеркивать не надо, такая строка будет искомой подпоследовательностью-палиндромом. Для последовательности из двух элементов возможны два варианта: если элементы равны, то мы имеем подпоследовательность-палиндром, ничего вычеркивать не надо. Если же элементы не равны, то вычеркиваем любой.
Пусть теперь нам дана подпоследовательность . Если первый и последний элементы подпоследовательности не совпадают, то один из них нужно вычеркнуть. Тогда у нас останется подпоследовательность или — то есть мы сведем задачу к подзадаче: . Если же первый и последний элементы равны, то мы можем оставить оба, но необходимо знать решение задачи .
Пример
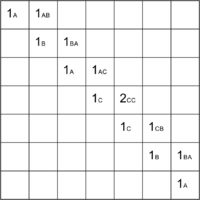
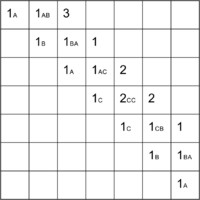
Рассмотрим решение на примере последовательности ABACCBA. Первым делом заполняем диагональ массива единицами, они будут соответствовать подпоследовательностями из одного элемента. Затем начинаем рассматривать подпоследовательности длины два. Во всех подпоследовательностях, кроме , элементы различны, поэтому в соответствующие ячейки запишем , а в — .
Получается, что мы будем заполнять массив по диагоналям, начиная с главной диагонали, ведущей из левого верхнего угла в правый нижний. Для подпоследовательностей длины получаются следующие значения: в подпоследовательности ABA первый и последний элемент равны, поэтому . В остальных подпоследовательностях первый и последний элементы различны.
BAC:
ACC:
CCB:
CBA:
Продолжая далее аналогичные рассуждения, заполним все ячейки под диагональю и в ячейке получим ответ .
Если же в задаче необходимо вывести не длину, а саму подпоследовательность-палиндром, то дополнительно к массиву длин мы должны построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован.
Размещаем граничные случаи: и , если . Теперь в рассматриваемой подстроке отделяем первый символ. Есть две возможности (какая из них реализуется, пока не знаем). Отделенный символ не участвует в образовании максимального подпоследовательности-палиндрома — тогда . Если же участвует, то ищем в подстроке с конца символ, совпадающий с отделенным (пусть его позиция ), тогда . Надо предусмотреть еще случай , а затем отсекать рекурсию. Получается следующая функция:
Function F(i, j)
if L[i, j] == -1
k = j
while S[i] <> S[k]
k--
R1 = F(i + 1, j)
if i <> k
R2 = F(i + 1, k - 1) + 2
else
R2 = 1
if R1 > R2
L[i, j] = R1
else
L[i, j] = R2
return L[i, j]