Алгоритм Борувки — различия между версиями
Watson (обсуждение | вклад) (→Описание алгоритма) |
Watson (обсуждение | вклад) |
||
| Строка 10: | Строка 10: | ||
| − | |||
| − | |||
==Реализация== | ==Реализация== | ||
| + | '''Псевдокод второго прохода: | ||
| + | {| width = 100% | ||
| + | |- | ||
| + | | | ||
| + | dfs(<tex>v, c, parent</tex>) | ||
| + | для всех вершин u смежных v: | ||
| + | если (<tex>u</tex> родитель) | ||
| + | переходим к следующей итерации | ||
| + | если (<tex>u</tex> не посещена) | ||
| + | если (<tex>return[u] >= enter[v]</tex>) | ||
| + | <tex>c2 \leftarrow</tex> новый цвет | ||
| + | <tex>col[vu] \leftarrow c2</tex> | ||
| + | dfs(<tex>u, c2, v</tex>) | ||
| + | иначе | ||
| + | <tex>col[vu] \leftarrow c</tex> | ||
| + | dfs(<tex>u, c, v</tex>) | ||
| + | иначе: | ||
| + | если (<tex>enter[u] <= enter[v]</tex>) | ||
| + | <tex>col[vu] \leftarrow c</tex> | ||
| + | start() | ||
| + | для всех v вершин графа: | ||
| + | если (<tex>v</tex> не посещена) | ||
| + | dfs(<tex>v, -1, -1</tex>) | ||
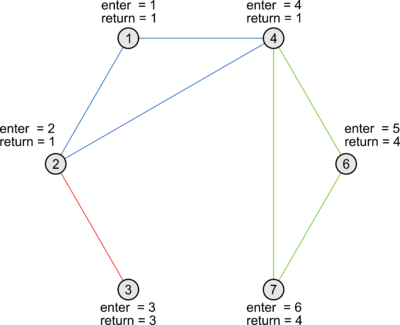
| + | |width = "310px" |[[Файл:Vertex_doubleconnection_1.png|thumb|center|400px|Компоненты обозначены разным цветом]] | ||
| + | |} | ||
| + | |||
<b>Вход</b>: граф <tex>G = (V, E)</tex><br> | <b>Вход</b>: граф <tex>G = (V, E)</tex><br> | ||
<b>Выход</b>: минимальный остов <tex>F</tex> графа <tex>G</tex><br> | <b>Выход</b>: минимальный остов <tex>F</tex> графа <tex>G</tex><br> | ||
Версия 00:43, 15 декабря 2012
Алгоритм Борувки — алгоритм поиска минимального остовного дерева (minimum spanning tree, MST) во взвешенном неориентированном связном графе. Впервые был опубликован в 1926 году Отакаром Борувкой.
Описание алгоритма
Пока не является деревом
- Для каждой компоненты связанности находим минимальное по весу ребро, которое связывает вершину из данной компоненты с вершиной, не принадлежащей данной компоненте.
- Добавим в все ребра, которые хотя бы для одной компоненты оказались минимальными.
Получившееся множество является минимальным остовным деревом графа .
Реализация
Псевдокод второго прохода:
dfs() для всех вершин u смежных v: если ( родитель) переходим к следующей итерации если ( не посещена) если () новый цвет dfs() иначе dfs() иначе: если () start() для всех v вершин графа: если ( не посещена) dfs() |
Вход: граф
Выход: минимальный остов графа
1)
1) Отсортируем по весу ребер.
2) Заведем систему непересекающихся множеств (DSU) и инициализируем ее множеством .
3) Перебирая ребра в порядке увеличения веса, смотрим, принадлежат ли и одному множеству. Если нет, то объединяем множества, в которых лежат и , и добавляем ребро к .
Асимптотика
Сортировка займет .
Работа с DSU займет , где - обратная функция Аккермана, которая не превосходит 4 во всех практических приложениях и которую можно принять за константу.
Алгоритм работает за .
Литература
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)