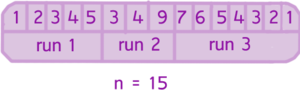Timsort — различия между версиями
(→Описание процедуры слияния) |
|||
| Строка 115: | Строка 115: | ||
Для вышеописанных массивов <tex> A, B </tex> алгоритм выглядит следующим образом: | Для вышеописанных массивов <tex> A, B </tex> алгоритм выглядит следующим образом: | ||
Первые 7 итераций сравниваются числа <tex>1, 2, 3, 4, 5, 6, 7</tex> из массива <tex>A</tex> с числом <tex>20000</tex>, так как <tex>20000</tex> больше, то элементы массива <tex>A</tex> копируются в результирующий. Начиная со следующей итерации алгоритм переходит в режим '''«галопа»''': сравнивает с числом <tex>20000</tex> последовательно элементы <tex>8, 10, 14, 22, 38, 7+2^{i - 1}, ..., 10000 </tex> массива <tex>A</tex>. (<tex> \thicksim\log_{2}(n)</tex> сравнений). После того как конец массива <tex>A</tex> достигнут и известно, что он весь меньше <tex>B</tex>, нужные данные из массива <tex>A</tex> копируются в результирующий. | Первые 7 итераций сравниваются числа <tex>1, 2, 3, 4, 5, 6, 7</tex> из массива <tex>A</tex> с числом <tex>20000</tex>, так как <tex>20000</tex> больше, то элементы массива <tex>A</tex> копируются в результирующий. Начиная со следующей итерации алгоритм переходит в режим '''«галопа»''': сравнивает с числом <tex>20000</tex> последовательно элементы <tex>8, 10, 14, 22, 38, 7+2^{i - 1}, ..., 10000 </tex> массива <tex>A</tex>. (<tex> \thicksim\log_{2}(n)</tex> сравнений). После того как конец массива <tex>A</tex> достигнут и известно, что он весь меньше <tex>B</tex>, нужные данные из массива <tex>A</tex> копируются в результирующий. | ||
| + | |||
| + | == Доказательство времени работы алгоритма == | ||
| + | Для оценки времени работы алгоритма '''Timsort''' составим рекуррентное соотношение. Пусть <tex> T(n) </tex> — время сортировки массива длины n. Рассмотрим последнее слияние двух подмассивов <tex> run1 </tex> и <tex> run2 </tex>: | ||
| + | |||
| + | <tex> T(n) = T(run1.size) + T(run2.size) + O(run1.size + run2.size) </tex>. Алгоритм построен таким образом, что сливаемые подмассивы имеют примерно равные размеры. Таким образом можно считать: | ||
| + | |||
| + | <tex> T(n) = T(run1.size) + T(run2.size) + O(run1.size + run2.size) </tex> <tex> \approx 2T(n/2) + O(n) \approx </tex> <tex> 4T(n/4) + 2O(n) \approx \dots \approx 2^{k}T(1) + kO(n) </tex>. | ||
| + | |||
| + | Осталось оценить <tex>k</tex>. <tex>n/minrun</tex> - количество сливаемых блоков, откуда следует, что <tex>2^{k} = n/minrun</tex>, значит <tex> k = log(n/minrun)</tex>. | ||
| + | |||
| + | <tex>T(n) \approx 2^{k}T(1) + kO(n) </tex> = <tex> log(n/minrun) + </tex><tex>log(n/minrun)O(n)</tex> <tex> = O(nlog(n)). </tex> | ||
| + | |||
== Источники == | == Источники == | ||
Версия 00:27, 9 июня 2013
Содержание
Timsort
Timsort — гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием.
Данный алгоритм был изобретен в 2002 году Тимом Петерсом(в честь него и назван). В настоящее время Timsort является стандартным алгоритмом сортировки в Python, OpenJDK 7 и реализован в Android JDK 1.5. Чтобы понять почему — достаточно взглянуть на таблицу из Википедии:
Основная идея алгоритма
По специальному алгоритму входной массив разделяется на подмассивы.
Каждый подмассив сортируется сортировкой вставками или сортировкой выбором.
Отсортированные подмассивы собираются в единый массив с помощью модифицированной сортировки слиянием.
Данный алгоритм основывается на том, что в реальном мире сортируемые массивы данных часто содержат в себе упорядоченные подмассивы. На таких данных Timsort существенно быстрее многих дргугих алгоритмов сортировки.
Алгоритм
Используемые понятия и комментарии
— размер входного массива.
— некоторый подмассив во входном массиве, который обязан быть упорядоченным одним из двух способов:
- строго по убыванию .
- нестрого по возрастанию .
— минимальный размер подмассива, описанного в предыдущем пункте.
Алгоритм Timsort состоит из нескольких шагов:
Шаг №1. Вычисление minrun
Число определяется на основе , исходя из принципов:
Оно не должно быть слишком большим, поскольку к подмассиву размера будет в дальнейшем применена сортировка вставками, а она эффективна только на небольших массивах.
Оно не должно быть слишком маленьким, так как чем меньше подмассив — тем больше итераций слияния подмассивов придётся выполнить на последнем шаге алгоритма. Оптимальная величина для — степень двойки. Это требование обусловлено тем, что алгоритм слияния подмассивов наиболее эффективно работает на подмассивах примерно равного размера.
Согласно авторским экспериментам:
- При нарушается пункт .
- При нарушается пункт .
- Наиболее эффективные значения из диапозона .
- Исключение — если , тогда и Timsort превращается в сортировку вставками.
Таким образом, алгоритм расчета не так уж сложен: берем старшие 6 бит числа и добавляем единицу, если в оставшихся младших битах есть хотя бы один ненулевой.
int GetMinrun(int n) {
int flag = 0; /* станет 1 если среди сдвинутых битов есть хотя бы 1 ненулевой */
while (n >= 64) {
flag |= n & 1;
n >>= 1;
}
return n + flag;
}
Шаг №2. Разбиения на подмассивы и их сортировка
На данном этапе у нас есть входной массив, его размер и вычисленное число . Алгоритм работы этого шага:- Указатель текущего элемента ставится в начало входного массива.
- Начиная с текущего элемента, идет поиск во входном массиве упорядоченного подмассива . По определению, в однозначно войдет текущий элемент и следующий за ним. Если получившийся подмассив упорядочен по убыванию — элементы переставляются так, чтобы они шли по возрастанию.
- Если размер текущего меньше , тогда выбираются следующие за найденным подмассивом элементы в количестве . Таким образом, на выходе будет получен подмассив размером большим или равный , часть которого (в лучшем случае — он весь) упорядочена.
- К данному подмассиву применяем сортировка вставками. Так как размер подмассива невелик и часть его уже упорядочена — сортировка работает эффективно.
- Указатель текущего элемента ставится на следующий за подмассивом элемент.
- Если конец входного массива не достигнут — переход к пункту 2, иначе — конец данного шага.
Шаг №3. Слияние
Если данные изначального массива достаточно близки к случайным, то размер упорядоченных подмассивов близок к . Если в изначальных данных были упорядоченные диапазоны, то упорядоченные подмассивы могут иметь размер, превышающий .
Итак, нужно объединить полученные подмассивы для получения результирующего упорядоченного массива. Для достижения эффективности, объединение должно удовлетворять требованиям:
- Объединять подмассивы примерно равного размера
- Сохранить стабильность алгоритма (не делать бессмысленных перестановок).
Алгоритм шага №3:
- Создается пустой стек пар <индекс начала подмассива> <размер подмассива>.
- Берется первый упорядоченный подмассив.
- Добавляется в стек пара данных <индекс начала текущего подмассива> <его размер>.
- При выполнении двух последующих правил выполняется процедура слияния текущего подмассива с предыдущими.
Если — размеры трёх верхних подмассивов в стеке, то:
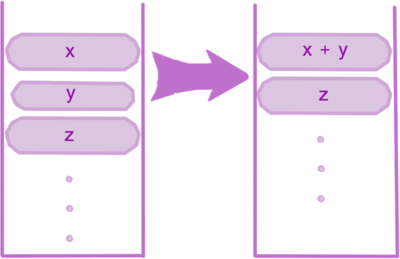
Если одно из правил нарушается — массив сливается с меньшим из массивов , . Процедура повторяется до выполнения обоих правил или полного упорядочивания данных. Если остались не рассмотренные подмассивы, то берется следующий и переходим ко второму пункту. Иначе — конец.
Основная цель этой процедуры — сохранение баланса. Изменения будут выглядеть как на картинке, а значит и размеры подмассивов в стеке эффективны для дальнейшей сортировки слиянием.
Описание процедуры слияния
Создается временный массив в размере меньшего из сливаемых подмассивов.
Меньший из подмассивов копируется во временный массив, но надо учесть, что если меньший подмассив правый, то ответ (результат сливания) формируется справа налево. Дабы избежать данной путаницы, лучше копировать всегда левый подмассив во временный. На скорости это практически не отразится.
Ставятся указатели текущей позиции на первые элементы большего и временного массива.
На каждом шаге рассматривается значение текущих элементов в большем и временном массивах, берется меньший из них, копируется в новый отсортированный массив. Указатель текущего элемента перемещается в массиве, из которого был взят элемент.
Предыдущий пункт повторяется, пока один из массивов не закончится.
Все элементы оставшегося массива добавляются в конец нового массива.
Модификация процедуры слияния подмассивов (Galloping Mode)
Рассмотрим процедуру слияния двух массивов:
Вышеуказанная процедура для них сработает, но каждый раз на её четвёртом пункте нужно будет выполнить одно сравнение и одно копирование. В итоге 10000 сравнений и 10000 копирований. Алгоритм Timsort предлагает в этом месте модификацию, которая получила называет «галоп». Алгоритм следующий:
Начинается процедура слияния.
На каждой операции копирования элемента из временного или большего подмассива в результирующий запоминается, из какого именно подмассива был элемент.
Если уже некоторое количество элементов (в данной реализации алгоритма это число равно 7) было взято из одного и того же массива — предполагается, что и дальше придётся брать данные из него. Чтобы подтвердить эту идею, алгоритм переходит в режим «галопа», то есть перемещается по массиву-претенденту на поставку следующей большой порции данных бинарным поиском (массив упорядочен) текущего элемента из второго соединяемого массива.
В момент, когда данные из текущего массива-поставщика больше не подходят (или был достигнут конец массива), данные копируются целиком.
Для вышеописанных массивов алгоритм выглядит следующим образом: Первые 7 итераций сравниваются числа из массива с числом , так как больше, то элементы массива копируются в результирующий. Начиная со следующей итерации алгоритм переходит в режим «галопа»: сравнивает с числом последовательно элементы массива . ( сравнений). После того как конец массива достигнут и известно, что он весь меньше , нужные данные из массива копируются в результирующий.
Доказательство времени работы алгоритма
Для оценки времени работы алгоритма Timsort составим рекуррентное соотношение. Пусть — время сортировки массива длины n. Рассмотрим последнее слияние двух подмассивов и :
. Алгоритм построен таким образом, что сливаемые подмассивы имеют примерно равные размеры. Таким образом можно считать:
.
Осталось оценить . - количество сливаемых блоков, откуда следует, что , значит .
=
Источники
Peter McIlroy "Optimistic Sorting and Information Theoretic Complexity", Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, ISBN 0-89871-313-7, Chapter 53, pp 467-474, January 1993.
Magnus Lie Hetland Python Algorithms: Mastering Basic Algorithms in the Python Language. — Apress, 2010. — 336 с.