Персистентный дек — различия между версиями
Shersh (обсуждение | вклад) м |
Shersh (обсуждение | вклад) (откамелкезил конспект; исправил согласно своим правилам) |
||
| Строка 1: | Строка 1: | ||
| − | '''Дек''' (англ. deque {{---}} double ended queue {{---}} очередь с двумя концами) {{---}} структура данных с двусторонним доступом к элементам, т.е. их можно удалять и добавлять как в начало, так и в конец дека. | + | '''Дек''' (англ. ''deque'' {{---}} double ended queue {{---}} очередь с двумя концами) {{---}} структура данных с двусторонним доступом к элементам, т.е. их можно удалять и добавлять как в начало, так и в конец дека. |
Кроме дека ещё существует структура данных, называемая ''steque'', которая представляет собой объединение стека и очереди - элементы можно добавлять только в один конец, а извлекать {{---}} с обоих. | Кроме дека ещё существует структура данных, называемая ''steque'', которая представляет собой объединение стека и очереди - элементы можно добавлять только в один конец, а извлекать {{---}} с обоих. | ||
| Строка 10: | Строка 10: | ||
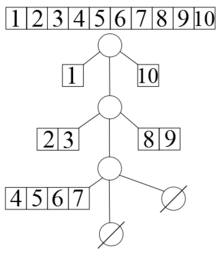
Персистентный дек можно визуально представить как односвязный список, где каждый узел хранит пару - левый элемент и правый, а также ''ребёнка'' {{---}} ссылку на следующий узел. Только левый и правый элемент каждого узла хранят в два раза больше объектов, чем предыдущий. Это удобно сделать с помощью типа ''пара''. | Персистентный дек можно визуально представить как односвязный список, где каждый узел хранит пару - левый элемент и правый, а также ''ребёнка'' {{---}} ссылку на следующий узел. Только левый и правый элемент каждого узла хранят в два раза больше объектов, чем предыдущий. Это удобно сделать с помощью типа ''пара''. | ||
| − | Тип <tex>Pair</tex> хранит пару элементов <tex>first</tex> и <tex>last</tex> типов <tex>T</tex>. | + | Тип <tex>\mathrm{Pair}</tex> хранит пару элементов <tex>first</tex> и <tex>last</tex> типов <tex>T</tex>. |
<code style = "display: inline-block;"> | <code style = "display: inline-block;"> | ||
| − | Pair< | + | Pair<T> { |
| − | + | T first | |
| − | + | T last | |
| − | } | + | } |
</code> | </code> | ||
| − | Сам дек можно инициализировать напрямую, вызвав конструктор <tex>Deque(left, ~child, ~right)</tex>, или через шаблоны <tex>Deque<T></tex>, тогда произойдёт следующее: | + | Сам дек можно инициализировать напрямую, вызвав конструктор <tex>\mathrm{Deque(left, ~child, ~right)}</tex>, или через шаблоны <tex>\mathrm{Deque<T>}</tex>, тогда произойдёт следующее: |
<code style = "display: inline-block;"> | <code style = "display: inline-block;"> | ||
| − | Deque< | + | Deque<T<> { |
| − | + | T left | |
| − | + | T right | |
| − | Deque<Pair< | + | Deque<Pair<T>> child |
| − | } | + | } |
</code> | </code> | ||
| − | Наша структура данных персистентна, следовательно операция <tex> | + | Наша структура данных персистентна, следовательно операция <tex> \mathrm{pushFront(x, ~D)} </tex> возвращает новый дек <tex> D' </tex> c элементом <tex> x </tex>, добавленным в начало <tex> D </tex>. |
| − | Пустой дек будем обозначать значком <tex> \emptyset </tex>, а пустую пару {{---}} <tex> \varnothing </tex>, чтобы было яснее, когда мы обращаемся к деку, а когда к элементу. Когда мы хотим добавить элемент в начало дека или удалить из начала, то прежде всего обращаемся к полю | + | Пустой дек будем обозначать значком <tex> \emptyset </tex>, а пустую пару {{---}} <tex> \varnothing </tex>, чтобы было яснее, когда мы обращаемся к деку, а когда к элементу. Когда мы хотим добавить элемент в начало дека или удалить из начала, то прежде всего обращаемся к полю <tex>left</tex>. Если же работаем с концом, то обращаемся сперва к полю <tex>right</tex>. |
<code> | <code> | ||
| − | + | '''pushFront'''(x, D) | |
| − | if D == <tex> \emptyset </tex> | + | '''if''' D == <tex> \emptyset </tex> |
// если дек пустой, то формируем новый дек | // если дек пустой, то формируем новый дек | ||
| − | return Deque(x, <tex> \emptyset ,~ \varnothing </tex>) | + | '''return''' Deque(x, <tex> \emptyset ,~ \varnothing </tex>) |
| − | else if D.left == <tex> \varnothing </tex> | + | '''else if''' D.left == <tex> \varnothing </tex> |
// если левый ребенок не существует, то сделаем <tex> x </tex> левым ребёнком | // если левый ребенок не существует, то сделаем <tex> x </tex> левым ребёнком | ||
| − | return Deque(x, D.child, D.right) | + | '''return''' Deque(x, D.child, D.right) |
| − | else | + | '''else''' |
// иначе объединим левого ребёнка с новым элементом и попытаемся добавить в дек на следующем уровне | // иначе объединим левого ребёнка с новым элементом и попытаемся добавить в дек на следующем уровне | ||
| − | return Deque(<tex> \varnothing </tex>, | + | '''return''' Deque(<tex> \varnothing </tex>, pushFront(Pair(x, D.left), D.child), D.right) |
</code> | </code> | ||
| − | Метод <tex> | + | Метод <tex> \mathrm{popFront(D)} </tex> возвращает пару <tex> \left \langle e, ~D' \right \rangle </tex> из первого элемента и нового дека, полученного из старого изъятием этого элемента. |
<code> | <code> | ||
| − | + | '''popFront'''(D) | |
| − | if D == <tex> \emptyset </tex> | + | '''if''' D == <tex> \emptyset </tex> |
// изъятие элемента из пустого дека возвращает пару "нулевой элемент {{---}} пустой дек" | // изъятие элемента из пустого дека возвращает пару "нулевой элемент {{---}} пустой дек" | ||
| − | return <tex> \mathcal{h} \varnothing ,~ \emptyset \mathcal{i} </tex> | + | '''return''' <tex> \mathcal{h} \varnothing ,~ \emptyset \mathcal{i} </tex> |
| − | else if D.left <tex> \neq ~\varnothing</tex> | + | '''else''' if D.left <tex> \neq ~\varnothing</tex> |
// если левый ребёнок не пуст, то возвращаем пару из него и нового дека без левого ребёнка, | // если левый ребёнок не пуст, то возвращаем пару из него и нового дека без левого ребёнка, | ||
// но если остался только левый ребёнок, но возвращаем его и пустой дек | // но если остался только левый ребёнок, но возвращаем его и пустой дек | ||
| − | if D.child = <tex> \emptyset </tex> and D.right = <tex> \varnothing </tex> | + | '''if''' D.child = <tex> \emptyset </tex> '''and''' D.right = <tex> \varnothing </tex> |
| − | return <tex> \mathcal{h} </tex>D.left, <tex> \emptyset \mathcal{i} </tex> | + | '''return''' <tex> \mathcal{h} </tex>D.left, <tex> \emptyset \mathcal{i} </tex> |
| − | return <tex> \mathcal{h} </tex>D.left, Deque(<tex> \varnothing </tex>, D.child, D.right)<tex> \mathcal{i} </tex> | + | '''return''' <tex> \mathcal{h} </tex>D.left, Deque(<tex> \varnothing </tex>, D.child, D.right)<tex> \mathcal{i} </tex> |
| − | else if D.child == <tex> \varnothing</tex> | + | '''else if''' D.child == <tex> \varnothing</tex> |
// если левый ребёнок оказался пуст, и при этом ссылка на следующий дек отсутствует, | // если левый ребёнок оказался пуст, и при этом ссылка на следующий дек отсутствует, | ||
// то вернём пару из правого ребёнка и абсолютно пустого дека | // то вернём пару из правого ребёнка и абсолютно пустого дека | ||
| − | return <tex> \mathcal{h} </tex>D.right, <tex>\emptyset \mathcal{i} </tex> | + | '''return''' <tex> \mathcal{h} </tex>D.right, <tex>\emptyset \mathcal{i} </tex> |
| − | else | + | '''else''' |
/* | /* | ||
| − | * если два предыдущих условия оказались не выполнены, то мы рекурсивно вызываем метод | + | * если два предыдущих условия оказались не выполнены, то мы рекурсивно вызываем метод <tex>\mathrm{popFront}</tex> |
| − | * и возвращённую пару "элемент {{---}} новый дек" сохраняем в переменные temp | + | * и возвращённую пару "элемент {{---}} новый дек" сохраняем в переменные <tex>temp</tex> и <tex>newDeque</tex>. |
| − | * Рекурсивные вызовы прекратятся, как только левый ребёнок окажется | + | * Рекурсивные вызовы прекратятся, как только левый ребёнок окажется не пустым |
| − | * или в деке будет отсутствовать ссылка на следующий дек | + | * или в деке будет отсутствовать ссылка на следующий дек. |
*/ | */ | ||
| − | temp, newDeque <tex> \leftarrow </tex> | + | temp, newDeque <tex> \leftarrow </tex> popFront(D.child) |
| − | if temp == <tex> \varnothing </tex> | + | '''if''' temp == <tex> \varnothing </tex> |
/* | /* | ||
* это возможно только тогда, когда в деке на максимальной глубине все элементы оказались пусты, | * это возможно только тогда, когда в деке на максимальной глубине все элементы оказались пусты, | ||
| − | * значит, мы сейчас на предпоследнем уровне, левый ребёнок пустой и child ссылается на абсолютно пустой дек, | + | * значит, мы сейчас на предпоследнем уровне, левый ребёнок пустой и <tex>child</tex> ссылается на абсолютно пустой дек, |
| − | * поэтому возвращаем right текущего дека и пустой дек | + | * поэтому возвращаем <tex>right</tex> текущего дека и пустой дек |
*/ | */ | ||
| − | return <tex> \mathcal{h} </tex>D.right, <tex>\emptyset \mathcal{i} </tex> | + | '''return''' <tex> \mathcal{h} </tex>D.right, <tex>\emptyset \mathcal{i} </tex> |
| − | else | + | '''else''' |
/* | /* | ||
| − | * если всё же temp не пуст, то надо вернуть первый элемент пары temp; | + | * если всё же <tex>temp</tex> не пуст, то надо вернуть первый элемент пары temp; |
| − | * в качестве left нового дека надо поставить temp.last (на уровне ниже temp хранил | + | * в качестве left нового дека надо поставить <tex>temp.last</tex> (на уровне ниже <tex>temp</tex> хранил |
| − | * в два раза больше элементов, поэтому на текущем уровне temp.last будет соответствовать | + | * в два раза больше элементов, поэтому на текущем уровне <tex>temp.last</tex> будет соответствовать |
| − | * требуемому количеству элементов); newDeque делаем child'ом | + | * требуемому количеству элементов); <tex>newDeque</tex> делаем <tex>child</tex>'ом |
| − | * нового дека, а right текущего right'ом нового | + | * нового дека, а <tex>right</tex> текущего <tex>right</tex>'ом нового |
*/ | */ | ||
| − | return <tex> \ | + | '''return''' <tex> \langle </tex>temp.first, Deque(temp.last, newDeque, D.right)<tex> \rangle </tex> |
</code> | </code> | ||
| Строка 93: | Строка 93: | ||
Рассмотрим поподробнее операции. В худшем случае элементы будут добавляться только в один конец, а извлекаться из другого. | Рассмотрим поподробнее операции. В худшем случае элементы будут добавляться только в один конец, а извлекаться из другого. | ||
| − | === | + | === pushFront === |
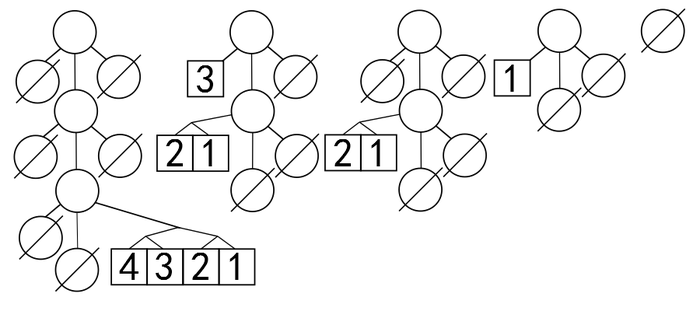
| − | Изначально у нас пустой дек. Элементы будем добавлять в левый конец дека и нумеровать согласно порядку добавления. Сначала добавим первый элемент. Он встанет на позицию левого ребёнка первого уровня дека. Теперь попытаемся добавить второй элемент. Позиция левого ребёнка занята, значит, мы объединяем новый элемент со старым и ставим сформированную пару на место левого ребёнка второго дека. Процесс добавления можно представить, как прибавление 1 к разряду числа в двоичном представлении: если в разряде 1, то подряд идущие за ней единицы обнулятся {{---}} элементы объединяются в пары, иначе становятся на место этого разряда. | + | Изначально у нас пустой дек. Элементы будем добавлять в левый конец дека и нумеровать согласно порядку добавления. Сначала добавим первый элемент. Он встанет на позицию левого ребёнка первого уровня дека. Теперь попытаемся добавить второй элемент. Позиция левого ребёнка занята, значит, мы объединяем новый элемент со старым и ставим сформированную пару на место левого ребёнка второго дека. Процесс добавления можно представить, как прибавление <tex>1</tex> к разряду числа в двоичном представлении: если в разряде <tex>1</tex>, то подряд идущие за ней единицы обнулятся {{---}} элементы объединяются в пары, иначе становятся на место этого разряда. |
[[Файл:PushDequeExample.png|700px]] | [[Файл:PushDequeExample.png|700px]] | ||
| − | === | + | === popFront === |
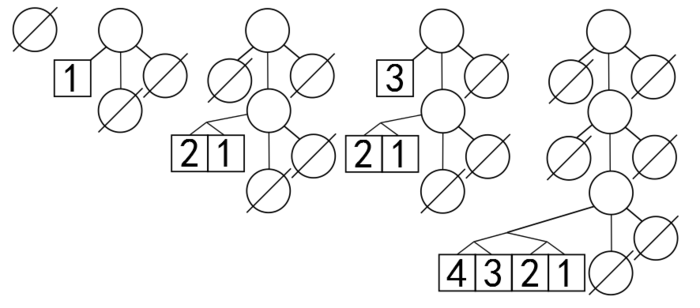
| − | Посмотрим, как работает | + | Посмотрим, как работает <tex>\mathrm{popFront}</tex> на примере дека, симметричного нашему предыдущему (в рисунке надо понять, что элементы хранятся слева направо: <tex>4 ~3 ~2 ~1</tex>). |
| − | Запустим первый <tex> | + | Запустим первый <tex> \mathrm{popFront} </tex>. Он будет рекурсивно вызывать сам себя, пока не дойдёт до последней ветки. Тогда в пару <tex> \left \langle temp, ~newDeque \right \rangle </tex> сохранятся две пары элементов и пустой дек высоты <tex>0</tex>. Так как <tex> temp </tex> не пуст, то в предыдущий рекурсивный вызов вернётся пара: в <tex>temp</tex> новый сохранится пара <tex>4 ~3</tex>, на текущем уровне будет пара <tex>2 ~1</tex>, а <tex> child </tex> будет ссылаться на пустой дек. Потом пара <tex>4 ~3</tex> передастся выше, <tex>child</tex> сохраняет ссылку на предыдущий дек, и, наконец, <tex>4</tex> извлечётся. И так далее. Аналогично добавлению, процесс извлечения элемента можно представить, как вычитание <tex>1</tex> из младшего разряда двоичного числа. |
[[Файл:PopDequeExample.png|700px]] | [[Файл:PopDequeExample.png|700px]] | ||
Версия 19:33, 11 ноября 2013
Дек (англ. deque — double ended queue — очередь с двумя концами) — структура данных с двусторонним доступом к элементам, т.е. их можно удалять и добавлять как в начало, так и в конец дека.
Кроме дека ещё существует структура данных, называемая steque, которая представляет собой объединение стека и очереди - элементы можно добавлять только в один конец, а извлекать — с обоих.
Эффективная реализация
Персистентный дек можно визуально представить как односвязный список, где каждый узел хранит пару - левый элемент и правый, а также ребёнка — ссылку на следующий узел. Только левый и правый элемент каждого узла хранят в два раза больше объектов, чем предыдущий. Это удобно сделать с помощью типа пара.
Тип хранит пару элементов и типов .
Pair<T> {
T first
T last
}
Сам дек можно инициализировать напрямую, вызвав конструктор , или через шаблоны , тогда произойдёт следующее:
Deque<T<> {
T left
T right
Deque<Pair<T>> child
}
Наша структура данных персистентна, следовательно операция возвращает новый дек c элементом , добавленным в начало .
Пустой дек будем обозначать значком , а пустую пару — , чтобы было яснее, когда мы обращаемся к деку, а когда к элементу. Когда мы хотим добавить элемент в начало дека или удалить из начала, то прежде всего обращаемся к полю . Если же работаем с концом, то обращаемся сперва к полю .
pushFront(x, D) if D == // если дек пустой, то формируем новый дек return Deque(x, ) else if D.left == // если левый ребенок не существует, то сделаем левым ребёнком return Deque(x, D.child, D.right) else // иначе объединим левого ребёнка с новым элементом и попытаемся добавить в дек на следующем уровне return Deque(, pushFront(Pair(x, D.left), D.child), D.right)
Метод возвращает пару из первого элемента и нового дека, полученного из старого изъятием этого элемента.
popFront(D) if D == // изъятие элемента из пустого дека возвращает пару "нулевой элемент — пустой дек" return else if D.left // если левый ребёнок не пуст, то возвращаем пару из него и нового дека без левого ребёнка, // но если остался только левый ребёнок, но возвращаем его и пустой дек if D.child = and D.right = return D.left, return D.left, Deque(, D.child, D.right) else if D.child == // если левый ребёнок оказался пуст, и при этом ссылка на следующий дек отсутствует, // то вернём пару из правого ребёнка и абсолютно пустого дека return D.right, else /* * если два предыдущих условия оказались не выполнены, то мы рекурсивно вызываем метод * и возвращённую пару "элемент — новый дек" сохраняем в переменные и . * Рекурсивные вызовы прекратятся, как только левый ребёнок окажется не пустым * или в деке будет отсутствовать ссылка на следующий дек. */ temp, newDeque popFront(D.child) if temp == /* * это возможно только тогда, когда в деке на максимальной глубине все элементы оказались пусты, * значит, мы сейчас на предпоследнем уровне, левый ребёнок пустой и ссылается на абсолютно пустой дек, * поэтому возвращаем текущего дека и пустой дек */ return D.right, else /* * если всё же не пуст, то надо вернуть первый элемент пары temp; * в качестве left нового дека надо поставить (на уровне ниже хранил * в два раза больше элементов, поэтому на текущем уровне будет соответствовать * требуемому количеству элементов); делаем 'ом * нового дека, а текущего 'ом нового */ return temp.first, Deque(temp.last, newDeque, D.right)
Операции добавления в правый конец и извлечение из него делаются симметрично.
Таким образом, если мы добавляем элементы только в один конец, то на -ом уровне дека не более элементов. Пусть глубина текущего дека Тогда в нём может находится не более объектов, откуда получаем .
Чтобы извлечь элемент, придётся спуститься не больше, чем на глубину дерева. Аналогично для добавления. Поэтому обе операции выполняются за
Пример
Рассмотрим поподробнее операции. В худшем случае элементы будут добавляться только в один конец, а извлекаться из другого.
pushFront
Изначально у нас пустой дек. Элементы будем добавлять в левый конец дека и нумеровать согласно порядку добавления. Сначала добавим первый элемент. Он встанет на позицию левого ребёнка первого уровня дека. Теперь попытаемся добавить второй элемент. Позиция левого ребёнка занята, значит, мы объединяем новый элемент со старым и ставим сформированную пару на место левого ребёнка второго дека. Процесс добавления можно представить, как прибавление к разряду числа в двоичном представлении: если в разряде , то подряд идущие за ней единицы обнулятся — элементы объединяются в пары, иначе становятся на место этого разряда.
popFront
Посмотрим, как работает на примере дека, симметричного нашему предыдущему (в рисунке надо понять, что элементы хранятся слева направо: ).
Запустим первый . Он будет рекурсивно вызывать сам себя, пока не дойдёт до последней ветки. Тогда в пару сохранятся две пары элементов и пустой дек высоты . Так как не пуст, то в предыдущий рекурсивный вызов вернётся пара: в новый сохранится пара , на текущем уровне будет пара , а будет ссылаться на пустой дек. Потом пара передастся выше, сохраняет ссылку на предыдущий дек, и, наконец, извлечётся. И так далее. Аналогично добавлению, процесс извлечения элемента можно представить, как вычитание из младшего разряда двоичного числа.