Декомпозиция Эдмондса-Галлаи — различия между версиями
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <tex>odd(G-U)</tex> - количество компонент связности нечетного размера в <tex> G[V - U]</tex>.}} | + | <tex>odd(G-U)</tex> - количество [[Отношение связности, компоненты связности|компонент связности]] нечетного размера в <tex> G[V - U]</tex>.}} |
{{Определение | {{Определение | ||
| Строка 7: | Строка 7: | ||
'''Дефицитом''' графа G мы будем называть величину: <br> | '''Дефицитом''' графа G мы будем называть величину: <br> | ||
<tex>\mathrm{def}(G) = |V| - 2\alpha (G)</tex>, <br> | <tex>\mathrm{def}(G) = |V| - 2\alpha (G)</tex>, <br> | ||
| − | где <tex>\alpha (G)</tex> - размер максимального поросочетания в <tex>G</tex>, а <br> | + | где <tex>\alpha (G)</tex> - размер [[Теорема о максимальном паросочетании и дополняющих цепях|максимального поросочетания]] в <tex>G</tex>, а <br> |
<tex>V(G)</tex> - множество вершин графа <tex>G</tex> | <tex>V(G)</tex> - множество вершин графа <tex>G</tex> | ||
}} | }} | ||
| Строка 40: | Строка 40: | ||
Необходимые определения: | Необходимые определения: | ||
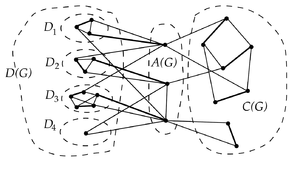
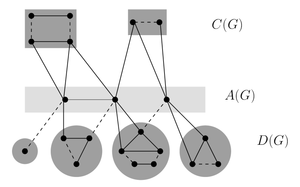
[[Файл: Edmonds-Gallai.png|300px|thumb|right|Пример. Рёбра из паросочетания выделены жирным]] | [[Файл: Edmonds-Gallai.png|300px|thumb|right|Пример. Рёбра из паросочетания выделены жирным]] | ||
| − | * <tex>D(G) = \{v \in V |</tex> существует максимальное паросочетание, не покрывающее <tex> v\}</tex> | + | * <tex>D(G) = \{v \in V |</tex> существует [[максимальное паросочетание|Теорема о максимальном паросочетании и дополняющих цепях]], не покрывающее <tex> v\}</tex> |
* <tex>A(G) = N(D(G)) \setminus D(G)</tex> | * <tex>A(G) = N(D(G)) \setminus D(G)</tex> | ||
* <tex>C(G) = V \setminus( D(G) \bigcup A(G) )</tex> | * <tex>C(G) = V \setminus( D(G) \bigcup A(G) )</tex> | ||
| Строка 64: | Строка 64: | ||
* <tex> \alpha (G - a) = \alpha (G) - 1.</tex> | * <tex> \alpha (G - a) = \alpha (G) - 1.</tex> | ||
|proof= | |proof= | ||
| − | Достаточно доказать, что <tex>D(G-a) = D(G)</tex>. <br> | + | Достаточно доказать, что <tex>D(G - a) = D(G)</tex>. <br> |
<tex>1)</tex> покажем, что <tex>D(G - a) \supset D(G)</tex> : <br> | <tex>1)</tex> покажем, что <tex>D(G - a) \supset D(G)</tex> : <br> | ||
| − | Пусть <tex>u \in D(G)</tex>. Тогда существует максимальное паросочетание <tex> | + | Пусть <tex>u \in D(G)</tex>. Тогда существует [[Теорема о максимальном паросочетании и дополняющих цепях|максимальное паросочетание]] <tex>M_u</tex> графа <tex>G</tex>, не покрывающее <tex>u</tex>. Поскольку любое максимальное паросочетание графа <tex>G</tex> покрывает a, то <tex> \alpha (G - a) = \alpha (G) - 1 </tex> и более того, если <tex> ax \in M_u </tex>, то <tex>_Mu \setminus {ax} </tex> - максимальное паросочетание графа <tex> G - a </tex>, не покрывающее <tex> u </tex>. Таким образом, <tex>D(G - a) \supset D(G) </tex>. <br> |
<tex>2)</tex>покажем, что <tex> D(G − a) \subset D(G)</tex>: <br> | <tex>2)</tex>покажем, что <tex> D(G − a) \subset D(G)</tex>: <br> | ||
| − | Предположим, что существует максимальное паросочетание <tex>M'</tex> графа<tex> G - a</tex>, не покрывающее вершину <tex>v not \in D(G)</tex>. Пусть <tex> w \in D(G) </tex>- смежная с<tex> a \in A(G)</tex> вершина, а <tex> | + | Предположим, что существует максимальное паросочетание <tex>M'</tex> графа <tex> G - a</tex>, не покрывающее вершину <tex>v not \in D(G)</tex>. Пусть <tex> w \in D(G) </tex> - смежная с <tex> a \in A(G)</tex> вершина, а <tex> M_w </tex>- максимальное паросочетание графа <tex> G </tex>, не покрывающее <tex> w </tex>. Так как <tex> v not \in D(G) </tex>, максимальное паросочетание <tex> M_w </tex> покрывает вершину <tex>v</tex>. Рассмотрим граф <tex> H = G(M_w \bigcup M') </tex> - очевидно, он является объединением нескольких путей и чётных циклов. Пусть <tex> U </tex> - компонента связности графа <tex> H </tex>, содержащая <tex>v</tex>. Так как <tex> dH(v) = 1 </tex>, то <tex> P = H(U) </tex> - путь с началом в вершине <tex>v</tex>. В пути <tex>P</tex> чередуются рёбра из <tex> M_w и M' </tex>, причём начинается путь ребром из <tex>M_w </tex>. Так как <tex> dH(a) = 1 </tex>, то вершина a либо не принадлежит пути <tex>P</tex>, либо является её концом (в этом случае последнее ребро пути принадлежит паросочетанию <tex> M_w</tex>). Рассмотрим несколько случаев: <br> |
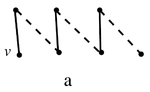
[[Файл: Gallai-lema-a.png|150px|thumb|right|случай '''а''']] | [[Файл: Gallai-lema-a.png|150px|thumb|right|случай '''а''']] | ||
'''a.''' Путь <tex>P</tex> кончается ребром из <tex> M'</tex> (см. рисунок)<br> | '''a.''' Путь <tex>P</tex> кончается ребром из <tex> M'</tex> (см. рисунок)<br> | ||
| − | Рассмотрим паросочетание <tex> | + | Рассмотрим паросочетание <tex>M_v = M_w \oplus E(P)</tex> (симметрическая разность |
| − | <tex> | + | <tex> M_w и E(P)</tex>. то есть, рёбра, входящие ровно в одно из двух множеств). |
| − | Очевидно, <tex> | + | Очевидно, <tex>M_v</tex> - максимальное паросочетание графа <tex>G</tex>, не покрывающее <tex>v</tex>, поэтому <tex> v \in D(G)</tex>, противоречие. <br> |
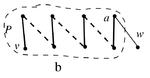
[[Файл: Gallai-lema-b.png|150px|thumb|right|случай '''b''']] | [[Файл: Gallai-lema-b.png|150px|thumb|right|случай '''b''']] | ||
| − | '''b.''' Путь <tex>P</tex> кончается ребром из <tex> | + | '''b.''' Путь <tex>P</tex> кончается ребром из <tex> M_w</tex>, вершина a - конец пути <tex>P</tex>. (см.рисунок)<br> |
| − | Рассмотрим паросочетание <tex> | + | Рассмотрим паросочетание <tex>M_v∗ = (M_w \oplus E(P)) \bigcup \{aw\} </tex>. Тогда <tex> M_v∗ </tex> - максимальное паросочетание графа <tex> G </tex>, не покрывающее <tex> v </tex>, поэтому <tex> v \in D(G) </tex>, противоречие. |
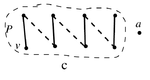
[[Файл: Gallai-lema-с.png|150px|thumb|right|случай '''c''']] | [[Файл: Gallai-lema-с.png|150px|thumb|right|случай '''c''']] | ||
| − | '''c.''' Путь <tex> P </tex> кончается ребром из <tex> | + | '''c.''' Путь <tex> P </tex> кончается ребром из <tex> M_w, a \in V(P) </tex> (см. рисунок) |
Рассмотрим паросочетание <tex> M'' = M \oplus E(P) </tex>. Тогда <tex> |M''| = |M'| + 1 </tex>, причём <tex>M'' \subset E(G - a)</tex>. Противоречие с максимальностью паросочетания <tex>M'</tex>. | Рассмотрим паросочетание <tex> M'' = M \oplus E(P) </tex>. Тогда <tex> |M''| = |M'| + 1 </tex>, причём <tex>M'' \subset E(G - a)</tex>. Противоречие с максимальностью паросочетания <tex>M'</tex>. | ||
| Строка 94: | Строка 94: | ||
|about = Галлаи, Эдмондс | |about = Галлаи, Эдмондс | ||
|statement= | |statement= | ||
| − | Пусть G - граф, <tex> | + | Пусть G - граф, <tex>U_1,{...},U_n</tex> - компоненты связности графа <tex>G(D(G))</tex>, <tex>D_i = G(U_i), C = G(C(G))</tex>. тогда: |
1) Граф <tex>C</tex> имеет совершенное паросочетание.<br> | 1) Граф <tex>C</tex> имеет совершенное паросочетание.<br> | ||
| − | 2) Графы <tex> | + | 2) Графы <tex>D_1,{...},D_n</tex> - фактор-критические. <br> |
| − | 3) Любое максимальное паросочетание <tex>M</tex> графа <tex>G</tex> состоит из совершенного паросочетания графа <tex>C</tex>, почти совершенных паросочетаний графов <tex> | + | 3) Любое максимальное паросочетание <tex>M</tex> графа <tex>G</tex> состоит из совершенного паросочетания графа <tex>C</tex>, почти совершенных паросочетаний графов <tex>D_1,{...},D_n</tex> и покрывает все вершины множества <tex>A(G)</tex> рёбрами с концами в различных компонентах связности <tex>U_1,{...},U_n</tex> <br> |
4) <tex>def(G) = n - |A(G)|, 2\alpha (G) = v(G) + |A(G)| - n</tex>. | 4) <tex>def(G) = n - |A(G)|, 2\alpha (G) = v(G) + |A(G)| - n</tex>. | ||
| Строка 112: | Строка 112: | ||
совершенное паросочетание графа <tex>C</tex>. Тем самым, мы доказали пункт 1). | совершенное паросочетание графа <tex>C</tex>. Тем самым, мы доказали пункт 1). | ||
| − | 2) Из формулы <tex> \alpha(G - A) = \alpha (G) - |A|</tex> следует, что <tex> | + | 2) Из формулы <tex> \alpha(G - A) = \alpha (G) - |A|</tex> следует, что <tex>U_1,{...},U_n</tex>- компоненты связности графа <tex>G - A</tex>. Для любой вершины <tex>u \in U_i </tex>существует максимальное паросочетание <tex>M_u</tex> графа <tex>G - A</tex>, не содержащее <tex>u</tex>. Так как <tex>U_i</tex> - компонента связности графа <tex>G - A</tex>, паросочетание <tex>M_u</tex> содержит максимальное паросочетание графа <tex>D_i</tex> (разумеется, не покрывающее вершину <tex>u</tex>). Следовательно, <tex> \alpha (D_i) = \alpha (D_i - u) </tex> и по теореме Галлаи(выше) мы получаем, что граф <tex>Di</tex> - фактор-критический. |
| − | 3) Пусть <tex>M</tex> - максимальное паросочетание графа <tex>G</tex>, а <tex>M'</tex> получено из <tex>M</tex> удалением всех рёбер, инцидентных вершинам множества <tex>A</tex>. Тогда <tex>|M'| \ge |M| - |A|</tex> и по формуле <tex> \alpha (G - A) = \alpha (G) - |A|</tex> понятно, что <tex>M'</tex> - максимальное паросочетание графа <tex>G - A</tex>. Более того, из <tex> \alpha (G - A) = \alpha (G) - |A|</tex> следует <tex>|M'| = |M| - |A|</tex>, а значит, все вершины множества <tex>A</tex> покрыты в <tex>M</tex> различными рёбрами. Так как <tex>M'</tex> - максимальное паросочетание графа <tex>G - A</tex>, то по пунктам 1) и 2) очевидно, что <tex>M'</tex> содержит совершенное паросочетание графа <tex>C</tex> и почти совершенные паросочетания фактор-критических графов <tex>D1,{...},Dn</tex>. Значит, рёбра паросочетания <tex>M</tex> соединяют вершины <tex>A</tex> с непокрытыми <tex>M'</tex> вершинами различных компонент связности из <tex> | + | 3) Пусть <tex>M</tex> - максимальное паросочетание графа <tex>G</tex>, а <tex>M'</tex> получено из <tex>M</tex> удалением всех рёбер, инцидентных вершинам множества <tex>A</tex>. Тогда <tex>|M'| \ge |M| - |A|</tex> и по формуле <tex> \alpha (G - A) = \alpha (G) - |A|</tex> понятно, что <tex>M'</tex> - максимальное паросочетание графа <tex>G - A</tex>. Более того, из <tex> \alpha (G - A) = \alpha (G) - |A|</tex> следует <tex>|M'| = |M| - |A|</tex>, а значит, все вершины множества <tex>A</tex> покрыты в <tex>M</tex> различными рёбрами. Так как <tex>M'</tex> - максимальное паросочетание графа <tex>G - A</tex>, то по пунктам 1) и 2) очевидно, что <tex>M'</tex> содержит совершенное паросочетание графа <tex>C</tex> и почти совершенные паросочетания фактор-критических графов <tex>D1,{...},Dn</tex>. Значит, рёбра паросочетания <tex>M</tex> соединяют вершины <tex>A</tex> с непокрытыми <tex>M'</tex> вершинами различных компонент связности из <tex>U_1,{...},U_n</tex>. |
4) Из пункта 3) сразу же следуют оба равенства пункта 4). | 4) Из пункта 3) сразу же следуют оба равенства пункта 4). | ||
Версия 15:42, 21 декабря 2013
| Определение: |
| - количество компонент связности нечетного размера в . |
| Определение: |
| Дефицитом графа G мы будем называть величину: , |
| Теорема (Бержа): |
Для любого графа G выполняется: |
| Теорема (Татта-Бержа): |
Дан граф , размер максимального паросочетания в нем равен: |
| Определение: |
| Множество , для которого , называется барьером. |
Структурная теорема Эдмондса-Галлаи
| Определение: |
Необходимые определения:
|
| Теорема (Галлаи): |
- фактор-критический граф - связен и для любой вершины выполняется равенство . |
| Лемма (Галлаи, о стабильности): |
Пусть Тогда:
|
| Доказательство: |
|
Достаточно доказать, что . a. Путь кончается ребром из (см. рисунок) b. Путь кончается ребром из , вершина a - конец пути . (см.рисунок) c. Путь кончается ребром из (см. рисунок) Рассмотрим паросочетание . Тогда , причём . Противоречие с максимальностью паросочетания .
|
| Теорема (Галлаи, Эдмондс): |
Пусть G - граф, - компоненты связности графа , . тогда:
1) Граф имеет совершенное паросочетание. |
| Доказательство: |
|
1) Последовательно удаляя вершины множества, по лемме о стабильности мы получим: Это означает, что не существует рёбер, соединяющих вершины из и . Каждое максимальное паросочетание графа покрывает все вершины множества , поэтому содержит совершенное паросочетание графа . Тем самым, мы доказали пункт 1). 2) Из формулы следует, что - компоненты связности графа . Для любой вершины существует максимальное паросочетание графа , не содержащее . Так как - компонента связности графа , паросочетание содержит максимальное паросочетание графа (разумеется, не покрывающее вершину ). Следовательно, и по теореме Галлаи(выше) мы получаем, что граф - фактор-критический. 3) Пусть - максимальное паросочетание графа , а получено из удалением всех рёбер, инцидентных вершинам множества . Тогда и по формуле понятно, что - максимальное паросочетание графа . Более того, из следует , а значит, все вершины множества покрыты в различными рёбрами. Так как - максимальное паросочетание графа , то по пунктам 1) и 2) очевидно, что содержит совершенное паросочетание графа и почти совершенные паросочетания фактор-критических графов . Значит, рёбра паросочетания соединяют вершины с непокрытыми вершинами различных компонент связности из . 4) Из пункта 3) сразу же следуют оба равенства пункта 4). |
| Утверждение (следствие из теоремы): |
- барьер графа |