Пересечение полуплоскостей, связь с выпуклыми оболочками

типа это одно и то же

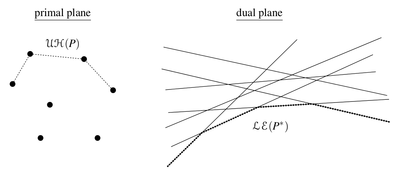
Короче говоря, верхний(нижний) конвекс-халл для множества точек, то же самое, что и нижняя(верхняя) огибающая(англ. lower(upper) envelope) для множества прямых.

Если рассмотреть что ребро [math] PQ [/math] принадлежит верхнему конвекс-халлу это означает, что все остальные точки лежат снизу. А если ребро [math] PQ [/math] принаджлежит нижней огибающей, то все остальные прямые лежат сверху. Короче да, одно и то же...

Если в конвекс-халле мы идем слева направо по увеличению икса, то тут то же самое будет, если мы пойдем справа налево по увеличению угла наклона.

Полностью считать пересечние можно по отдельности (верхняя + нижняя огибающая), а можно и сразу все, как полный конвекс-халл.

Тут бы и закончить конспект, но стоит уточнить, что у пересечения полуплоскостей есть одна небольшая особенность — оно может быть пусто, тогда как выпуклая оболочка вполне себе всегда определена, и это надо учитывать. И еще. когда мы рассматриваем верхнюю(нижнюю) огибающую, мы рассматриваем все прямые кроме вертикальных. Еще прямые близкие к вертикальным, но имеющие разный наклон (/ и \) are mapped to very different points. Отсюда выходит то, почему конвекс-халл состоит из двух таких разных и одинаковых частей.

Короче есть биекция [math] D [/math] между точками и прямыми.

[math] D(P(k, b)) = (Y = kX - b) [/math]

[math] D(Y = kX + b) = P(k, -b) [/math]

[math] D(D(P)) = P [/math]

В общем алгоритм такой. Отдельно строим конвех-халл для плоскостей смотрящих вверх и для смотрящих вниз. Получаем две цепочки. Пересекаем их пуская заметающую вертикальную прямую

Источники

• Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars (2008), Computational Geometry: Algorithms and Applications (3rd edition), Springer-Verlag, ISBN 978-3-540-77973-5 Chapter 15 page 253-254
• http://wwwisg.cs.uni-magdeburg.de/ag/lehre/SS2012/GAG/slides/V12.pdf