Динамическая выпуклая оболочка (достаточно log^2 на добавление/удаление) — различия между версиями
Dima (обсуждение | вклад) |
Dima (обсуждение | вклад) (→Левая и правая выпуклые оболочки) |
||
| Строка 8: | Строка 8: | ||
== Левая и правая выпуклые оболочки == | == Левая и правая выпуклые оболочки == | ||
| − | Определим левую (правую) выпуклую оболочку множества точек <tex>P</tex>, как выпуклую оболочку множества <tex>P \cup \{\infty_+\}</tex> <tex>(P \cup \{\infty_-\})</tex>, где <tex>\infty_- = (-\infty, 0), \infty_+ = (+\infty, 0)</tex>. Тогда задачу можно свести к поддержанию отдельно левой и правой выпуклых оболочек. Далее будем рассматривать только динамическое поддержание левой оболочки (далее, для краткости, будем называть её просто выпуклой оболочкой). | + | Определим левую (правую) выпуклую оболочку множества точек <tex>P</tex>, как выпуклую оболочку множества <tex>P \cup \{\infty_+\}</tex> <tex>(P \cup \{\infty_-\})</tex>, где <tex>\infty_- = (-\infty, 0), \infty_+ = (+\infty, 0)</tex>. Тогда задачу можно свести к поддержанию отдельно левой и правой выпуклых оболочек. Далее будем рассматривать только динамическое поддержание левой оболочки (далее, для краткости, будем называть её просто выпуклой оболочкой). Заметим также, что точки вдоль выпуклой оболочки отсортированы по ординате. |
[[Файл:Lc_rc.png|400px|thumb|center|Левая и правая выпуклые оболочки некоторого множества точек]] | [[Файл:Lc_rc.png|400px|thumb|center|Левая и правая выпуклые оболочки некоторого множества точек]] | ||
| + | |||
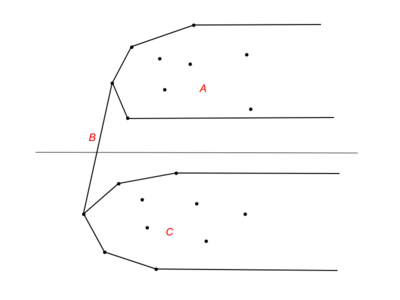
| + | [[Файл:Bridge_hull.png|400px|thumb|center|Мост между двумя выпуклыми оболочками, разделенными горизонтальной прямой]] | ||
| + | |||
| + | {|border="0" cellpadding="5" width=30% align=center | ||
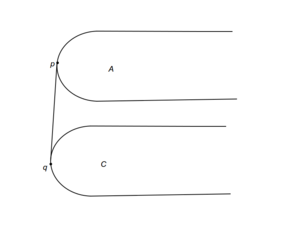
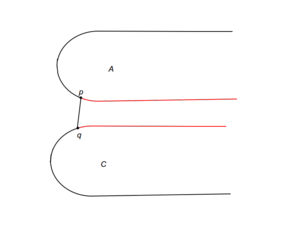
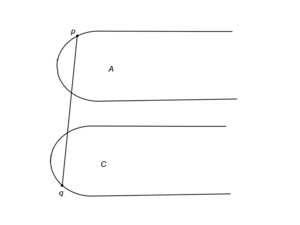
| + | |[[Файл: Case_a.png|thumb|300px|center|a. Касательная найдена]] | ||
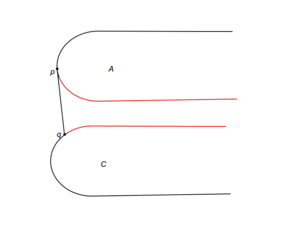
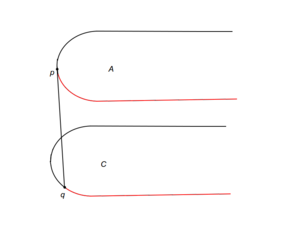
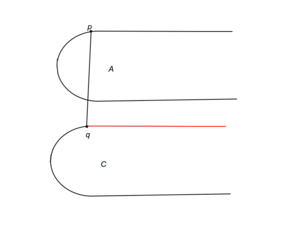
| + | |[[Файл: Case_b.png|thumb|300px|center|b. Может быть отброшена часть C после q, а также часть A перед p]] | ||
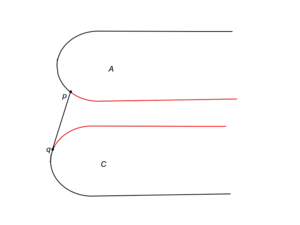
| + | |[[Файл: Case_c.png|thumb|300px|center|c. Может быть отброшена часть C перед q, а также часть A перед p]] | ||
| + | | | ||
| + | |} | ||
| + | |||
| + | {|border="0" cellpadding="5" width=30% align=center | ||
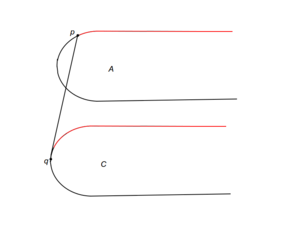
| + | |[[Файл: Case_d.png|thumb|300px|center|d. По аналогии со случаем b]] | ||
| + | |[[Файл: Case_e.png|thumb|300px|center|e. По аналогии со случаем c]] | ||
| + | |[[Файл: Case_f.png|thumb|300px|center|f. Может быть отброшена часть C после q, а также часть A перед p]] | ||
| + | | | ||
| + | |} | ||
| + | |||
| + | {|border="0" cellpadding="5" width=30% align=center | ||
| + | |[[Файл: Case_g.png|thumb|300px|center|g. Только часть C после q может быть отброшена]] | ||
| + | |[[Файл: Case_h.png|thumb|300px|center|h. По аналогии со случаем h]] | ||
| + | |[[Файл: Case_i.png|thumb|300px|center|i. В этом случае нельзя сразу сказать, какие части A и C могут быть отброшены. Случай дробится на два]] | ||
| + | | | ||
| + | |} | ||
== Структура данных == | == Структура данных == | ||
Версия 03:39, 29 марта 2014
Пусть дано множество точек , изначально пустое, и последовательность точек , которые последовательно добавляются или удаляются из (естественно, точка может быть удалена, если она уже принадлежит ). Требуется динамически поддерживать выпуклую оболочку .
В статье описан алгоритм, требующий времени на добавление/удаление точки.
Содержание
Левая и правая выпуклые оболочки
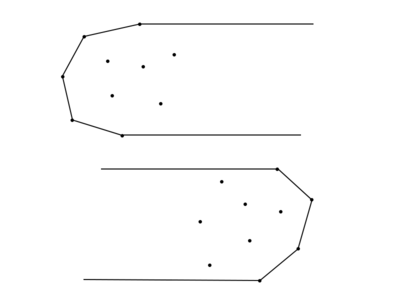
Определим левую (правую) выпуклую оболочку множества точек , как выпуклую оболочку множества , где . Тогда задачу можно свести к поддержанию отдельно левой и правой выпуклых оболочек. Далее будем рассматривать только динамическое поддержание левой оболочки (далее, для краткости, будем называть её просто выпуклой оболочкой). Заметим также, что точки вдоль выпуклой оболочки отсортированы по ординате.
Структура данных
Будем хранить отсортированные лексикографически () точки в листьях сбалансированного бинарного дерева поиска (например, красно-черного или AVL). Во внутренних вершинах будем хранить вспомогательную информацию: во-первых, наименьшую точку в поддереве с корнем в данной вершине; а во-вторых, пару точек, определяющих общую касательную к выпуклым оболочкам точек левого и правого поддеревьев данной вершины (будем называть такую пару точек мостом).
Операции
Получение выпуклой оболочки
Принадлежность точки выпуклой оболочке
Вставка точки
Удаление точки
Источники
- Реализация Антона Ковшарова
- Ф. Препарата, М. Шеймос. Вычислительная геометрия (1989). стр. 151 (тут описан более сложный алгоритм с двухуровневой структурой данных, но с такой же асимптотикой)
- Overmars, M. H.; van Leeuwen, J. (1981), "Maintenance of configurations in the plane" (и тут тоже)