Вещественный двоичный поиск — различия между версиями
(→Примеры использования) |
(→Псевдокод) |
||
| Строка 26: | Строка 26: | ||
== Псевдокод == | == Псевдокод == | ||
| − | < | + | <code> |
| − | findLeft(c): | + | '''findLeft'''(c): |
x = -1 | x = -1 | ||
| − | while f(x) > c | + | '''while''' f(x) > c |
x = x * 2 | x = x * 2 | ||
| − | return x | + | '''return''' x |
| − | </ | + | </code> |
| − | < | + | <code> |
| − | findRight(c): | + | '''findRight'''(c): |
x = 1 | x = 1 | ||
| − | while f(x) < c | + | '''while''' f(x) < c |
x = x * 2 | x = x * 2 | ||
| − | return x | + | '''return''' x |
| − | </ | + | </code> |
| − | < | + | <code> |
| − | binSearch(c): | + | '''binSearch'''(c): |
| − | left = findLeft(с) | + | left = '''findLeft'''(с) |
| − | right = findRight(с) | + | right = '''findRight'''(с) |
| − | while left < right - eps //Здесь можно использовать другое условие выхода | + | '''while''' left < right - eps //Здесь можно использовать другое условие выхода |
mid = (left + right) / 2 | mid = (left + right) / 2 | ||
| − | if f(mid) == c //** | + | '''if''' f(mid) == c //** |
| − | return mid //** | + | '''return''' mid //** |
| − | else if f(mid) < c | + | '''else if''' f(mid) < c |
left = mid | left = mid | ||
| − | else | + | '''else''' |
right = mid | right = mid | ||
| − | return l | + | '''return''' l |
| − | </ | + | </code> |
== Примеры использования == | == Примеры использования == | ||
Версия 08:01, 10 июня 2014
Вещественный двоичный поиск — алгоритм поиска аргумента для заданного значения монотонной вещественной функции.
Содержание
Формулировка задачи
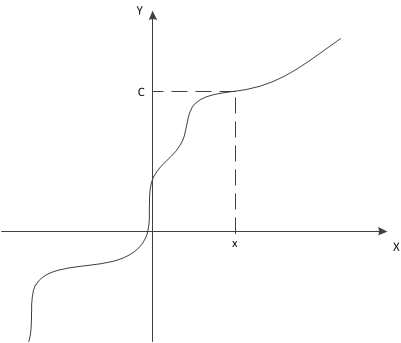
Пусть нам задана монотонная функция. Необходимо найти значение аргумента этой функции, в которой она принимает определенное значение .
Решение задачи
Применим идею двоичного поиска. Выберем такие границы, где значение функции точно больше и точно меньше заданного значения. Выберем значение в середине этого отрезка. Если оно меньше, чем заданное, то сместим левую границу в середину отрезка. В противном случае сместим правую границу. Далее повторим процесс сужения границ. Встает вопрос, когда остановиться. Есть несколько способов сделать это.
Способы закончить поиск
| Способы | Плюсы | Минусы | Оценка на число итераций |
|---|---|---|---|
| 1) Окончание, когда рассматриваемый отрезок станет меньше заданного эпсилон (= ). | Заданная точность найденного значения. | Алгоритм может зациклиться. В компьютере мы работаем с конечным числом вещественных чисел, у которых есть точность. При больших значениях функции длина отрезка может никогда не уменьшиться до заданного значения. | В данном случае нам нужно рассмотреть чисел => примерное число итераций . |
| 2) Окончание, когда значение функции на концах отрезках различается менее, чем на заданное эпсилон (= ). | Значение функции от найденного значения имеет заданную точность. | а) Возможна большая погрешность, если функция будет очень медленно возрастать. б) Алгоритм может зациклиться. В компьютере мы работаем с конечным числом вещественных чисел, у которых есть точность. При быстром возрастании значений функции мы можем не найти такие границы, что значение на них различается менее, чем на заданное . |
Аналогичная с первым случаем логика, примерное число итераций . |
| 3) «Абсолютно точный поиск» Окончание, когда границы отрезка — два соседних по представлению значения в типе данных. Утверждается, что два числа — соседние, если середина их отрезка совпадает или с левой, или с правой границей. |
Максимально возможная точность найденного значения. | Возможно плохое поведение, если искомый аргумент равен нулю. | При работе с числами с плавающей точкой количество итераций зависит от плотности чисел на данном отрезке. При работе с числами фиксированной точности (= ) количество итераций аналогично первому и второму случаю равно . |
| 4) «Итеративный способ» Выполнение конечного числа итераций. |
У способа фиксированная погрешность. | Довольно плохая точность, если границы отрезка находятся на большом расстоянии. | Выполняется заданное количество итераций. |
Выбор границы отрезка для поиска
Для начала найдем правую границу. Выберем произвольную положительную точку (например ). Будем удваивать ее до тех пор, пока значение функции в этой точке меньше заданного. Для того, чтобы найти левую границу выберем произвольную отрицательную точку (например ). Будем удваивать ее до тех пор, пока значение в ней будет больше заданного значения.
Псевдокод
findLeft(c):
x = -1
while f(x) > c
x = x * 2
return x
findRight(c):
x = 1
while f(x) < c
x = x * 2
return x
binSearch(c):
left = findLeft(с)
right = findRight(с)
while left < right - eps //Здесь можно использовать другое условие выхода
mid = (left + right) / 2
if f(mid) == c //**
return mid //**
else if f(mid) < c
left = mid
else
right = mid
return l
Примеры использования
- Классической задачей на вещественный двоичный поиск является задача поиска корня -ой степени из числа : . При нижней границей для поиска будет , а верхней — .
- Если функция нестрого монотонна, то, убрав из приведенного выше алгоритма строки, отмеченные , мы получим алгоритм, который будет находить такой, что и .
Замечания
- Необходимо отметить, то функция должна быть строго монотонна, если мы ищем конкретный корень и он единственный. Нестрого монотонна, если нам необходимо найти самый левый (правый) аргумент. Если же функция не монотонна, то данный алгоритм не найдет искомый аргумент, либо найдет аргумент, но он не будет единственным.
- Важным отличием от целочисленного поиска является то, что мы передвигаем границу ровно в середину отрезка (), а не со смещением внутрь отрезка ().