Прямое произведение ДКА

Определение:

Прямым произведением двух ДКА [math]A_1 = \langle \Sigma, Q_1, s_1, T_1, \delta_1 \rangle[/math] и [math]A_2 = \langle \Sigma, Q_2, s_2, T_2, \delta_2 \rangle[/math] называется ДКА [math]A = \langle \Sigma, Q, s, T, \delta \rangle[/math], где: [math]Q = Q_1 \times Q_2,[/math] [math]s = \langle s_1, s_2 \rangle,[/math] [math]T = T_1 \times T_2,[/math] [math]\delta(\langle q_1, q_2 \rangle, c) = \langle \delta_1(q_1, c), \delta_2(q_2, c) \rangle.[/math]

Пример

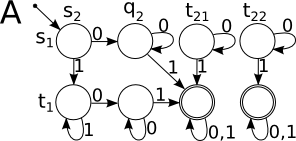
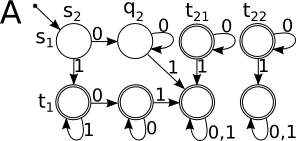
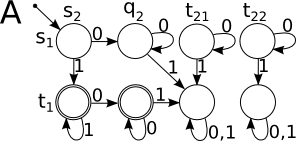
Возьмем автомат [math]A_1 = \langle \Sigma = \lbrace 0, 1 \rbrace, Q_1 = \lbrace s_1, t_1 \rbrace, s_1, T_1 = \lbrace t_1 \rbrace, \delta_1 \rangle[/math], и автомат [math]A_2 = \langle \Sigma = \lbrace 0, 1 \rbrace, Q_2 = \lbrace s_2, q_2, t_{21}, t_{22} \rbrace, s_2, T_2 = \lbrace t_{21}, t_{22} \rbrace, \delta_2 \rangle[/math].

Автомат [math]A = \langle \Sigma, Q, s, T, \delta \rangle[/math] будет их пересечением.

Согласно определению:

1. [math]\Sigma = \lbrace 0, 1 \rbrace[/math]
2. [math]Q = \lbrace \langle s_1, s_2 \rangle, \langle s_1, q_2 \rangle, \langle s_1, t_{21} \rangle, \langle s_1, t_{22} \rangle, \langle t_1, s_2 \rangle, \langle t_1, q_2 \rangle, \langle t_1, t_{21} \rangle, \langle t_1, t_{21} \rangle \rbrace[/math]
3. [math]s = \langle s_1, s_2 \rangle[/math]
4. [math]T = \lbrace \langle t_1, t_{21} \rangle, \langle t_1, t_{22} \rangle \rbrace[/math]
5. [math]\delta :[/math]
   • [math]\delta(\langle s_1, s_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(s_2, 0) \rangle = \langle s_1, q_2 \rangle [/math]
   • [math]\delta(\langle s_1, s_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(s_2, 1) \rangle = \langle t_1, s_2 \rangle [/math]
   • [math]\delta(\langle s_1, q_2 \rangle, 0) = \langle \delta_1(s_1, 0), \delta_2(q_2, 0) \rangle = \langle s_1, q_2 \rangle [/math]
   • [math]\delta(\langle s_1, q_2 \rangle, 1) = \langle \delta_1(s_1, 1), \delta_2(q_2, 1) \rangle = \langle t_1, t_{21} \rangle [/math]
   • ...

Применение

Изменив конструкцию, можно получить автомат, допускающий разность или объединение двух языков.

Объединение ДКА

Необходимо разрешать любую цепочку, удовлетворяющую первому или второму автомату, для этого сделаем терминальными следующие вершины [math]T = (T_1 \times Q_2) \cup (Q_1 \times T_2)[/math]. Полученный автомат удовлетворяет нашим требованиям, так как попав в какое-либо состояние из [math]T_1[/math] или [math]T_2[/math], цепочка будет удовлетворять первому или второму автомату соответственно.

Разность ДКА

Рассмотрим автомат [math]\overline{M} = \langle \Sigma , Q , s , Q \setminus T , \delta \rangle [/math], то есть автомат [math]M[/math], в котором терминальные и нетерминальные состояния инвертированы. Очевидно, он допускает те и только те слова, которые не допускает автомат [math]M[/math], а значит, задаёт язык [math]\overline{M}[/math]. Таким образом, [math]\overline{M}[/math] — регулярный.

Заметим, что если [math]L[/math] и [math]M[/math] - регулярные языки, то [math]L \setminus M = L \cap \overline{M}[/math] - так же регулярный.

Таким образом, надо построить пересечение двух автоматов, предварительно инвертировав во втором терминальные и нетерминальные состояния. Заметим, что меняется только набор терминальных вершин, следовательно в итоговой конструкции произведения ДКА сделаем терминальными следующие вершины [math]T = T_1 \times (Q_2 \setminus T_2)[/math].

См. также

• Детерминированные конечные автоматы
• Замкнутость регулярных языков относительно различных операций

Источники информации

• Wikipedia — Deterministic finite automaton
• [[http://www.andrew.cmu.edu/user/ko/pdfs/lecture-3.pdf | FORMAL LANGUAGES, AUTOMATA AND COMPUTATION : Carnegie Mellon University in Qatar

]]

• Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 152-154.