Эквивалентность состояний ДКА — различия между версиями
Shersh (обсуждение | вклад) (→Основные определения) |
Shersh (обсуждение | вклад) (→Проверка ДКА на эквивалентность) |
||
| Строка 35: | Строка 35: | ||
== Проверка ДКА на эквивалентность == | == Проверка ДКА на эквивалентность == | ||
Заданы два автомата: <tex> \mathcal{A}_1 </tex> со стартовым состоянием <tex> s_1 </tex> и <tex> \mathcal{A}_2 </tex> со стартовым состоянием <tex> s_2 </tex> соответственно. Нужно проверить их на эквивалентность. | Заданы два автомата: <tex> \mathcal{A}_1 </tex> со стартовым состоянием <tex> s_1 </tex> и <tex> \mathcal{A}_2 </tex> со стартовым состоянием <tex> s_2 </tex> соответственно. Нужно проверить их на эквивалентность. | ||
| + | |||
| + | '''Замечание:''' для реализации оба автомата обязательно должны иметь [[Детерминированные_конечные_автоматы#допускает|дьявольские состояния]]. | ||
=== Проверка через минимизацию === | === Проверка через минимизацию === | ||
Для этого построим автомат <tex> \mathcal{A} </tex>, содержащий все состояния обоих автоматов и изначальные переходы между ними. Стартовым состоянием в новом автомате можно сделать <tex> s_1 </tex> или <tex> s_2 </tex> — это не имеет значения. При этом состояния одного из автоматов станут недостижимыми из новый стартовой вершины в новом автомате, но для алгоритма это и не важно.<br> | Для этого построим автомат <tex> \mathcal{A} </tex>, содержащий все состояния обоих автоматов и изначальные переходы между ними. Стартовым состоянием в новом автомате можно сделать <tex> s_1 </tex> или <tex> s_2 </tex> — это не имеет значения. При этом состояния одного из автоматов станут недостижимыми из новый стартовой вершины в новом автомате, но для алгоритма это и не важно.<br> | ||
| Строка 41: | Строка 43: | ||
Также можно минимизировать каждый автомат отдельно и проверить минимизированные версии на изоморфизм. | Также можно минимизировать каждый автомат отдельно и проверить минимизированные версии на изоморфизм. | ||
| − | |||
| − | |||
=== Проверка через BFS === | === Проверка через BFS === | ||
| − | + | Два автомата можно также проверить на эквивалентность, используя [[Обход в ширину | обход в ширину]]. Будем синхронно обходить два автомата, начиная со стартовых состояний, в поисках такой строки, которая различает два состояний этих автоматов. То есть она будет допускаться одним автоматом, но не будет принадлежать языку другого. | |
| − | |||
| + | Поскольку эквивалентные автоматы допускают один тот же язык, при переходе по одним и тем же символам в обоих автоматах, слово должно приниматься обоими автоматами одновременно. То есть вершины, в которые мы перешли, должны быть либо одновременно терминальными, либо одновременно нетерминальными, что и проверяет приведённый алгоритм. | ||
| + | ==== Псевдокод ==== | ||
<wikitex> | <wikitex> | ||
| − | + | <font color=green>// $\mathtt{aut}[i][c]$ {{---}} номер состояния, в которое есть переход из состояния $i$ по символу $c$</font> | |
| − | <font color=green>// | + | '''boolean''' $\mathtt{bfsEquivalenceCheck}$($\mathtt{aut1}$ : '''int[][]''', $\mathtt{aut2}$ : '''int[][]'''): |
| − | ''boolean | + | $Q.\mathtt{push}(\langle s_1, s_2 \rangle) $ <font color=green>// <tex>Q</tex> {{---}} очередь из пар состояний</font> |
| − | $Q.push( \langle s_1, s_2 \rangle ) $ | + | $\mathtt{used1}[s_1] \leftarrow $ ''true'' |
| − | $\mathtt{used1[s_1] | + | $\mathtt{used2}[s_2] \leftarrow $ ''true'' |
| − | $\mathtt{used2[s_2] | + | '''while''' $Q \ne \varnothing $ |
| − | '''while''' $Q \ne \varnothing $ | + | $u, v \leftarrow Q.\mathtt{pop}()$ |
| − | $u | + | '''if''' $\mathtt{isTerminal1[u]} \ne \mathtt{isTerminal2[v]}$ |
| − | |||
| − | |||
| − | '''if''' | ||
'''return''' ''false'' | '''return''' ''false'' | ||
| − | '''for''' $ | + | '''for''' $c \in \Sigma$ |
| − | '''if''' | + | '''if''' '''not''' $\mathtt{used1[aut1}[u][c]]$ '''or''' '''not''' $\mathtt{used2[aut2}[v][c]]$ |
| − | $Q.push( \langle \mathtt{aut1[u][ | + | $Q.\mathtt{push}(\langle \mathtt{aut1}[u][c], \mathtt{aut2}[v][c] \rangle)$ |
| − | $\mathtt{used1[aut1[u][ | + | $\mathtt{used1[aut1}[u][c]] \leftarrow $ ''true'' |
| − | $\mathtt{used2[aut2[v][ | + | $\mathtt{used2[aut2}[v][c]] \leftarrow $ ''true'' |
| − | '''return''' true | + | '''return''' ''true'' |
| − | + | ||
| + | Корректность алгоритма следует из строго доказательства того факта, что если два состояния $u$ и $v$ различаются какой-то строкой, то они различаются строкой длины $O(n)$. | ||
| − | + | Интуитивное понимание алгоритма такое: пусть по строке $w$ мы пришли в состояния $ \langle u, v \rangle $, и пусть они оба нетерминальные. После этого совершим переход по символу $c$ в состояния $ \langle u', v' \rangle $. | |
| − | + | Тогда если $\mathtt{isTerminal1[u']} \ne \mathtt{isTerminal2[v']}$, то строка $wc$ различает эти два состояния. А значит автоматы не эквивалентны. | |
| − | |||
| − | |||
| − | |||
| − | Тогда если $\mathtt{isTerminal1[u]} \ne \mathtt{isTerminal2[v]}$, то строка $wc$ различает эти два состояния. А значит автоматы не эквивалентны. | ||
</wikitex> | </wikitex> | ||
Версия 20:53, 18 октября 2014
Содержание
Связь эквивалентности состояний и различимости состояний
| Определение: |
| Два автомата и называются эквивалентными (англ. equivalent), если они распознают один и тот же язык над алфавитом , то есть . |
| Определение: |
Слово различает (англ. distinguish) два состояния и , если
|
| Определение: |
Два состояния и называются эквивалентными , если не существует строки, которая их различает, то есть верно, что
|
Заметим, что эквивалентность состояний действительно является отношением эквивалентности. Так как (равносильность) является отношением эквивалентности и в детерминированном автомате всегда существует путь по любому слову, описанное нами отношение является отношением эквивалентности.
| Лемма: |
, , , различает и . Тогда различает и . |
| Доказательство: |
|
А значит, по условию различимости для и , |
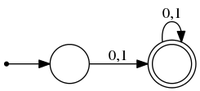
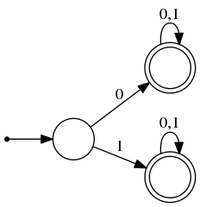
Пример
Эти два автомата принимают слова из языка слов длины не меньше одного, состоящих из символов алфавита . Стартовые и все допускающие состояния автоматов эквивалентны между собой.
Проверка ДКА на эквивалентность
Заданы два автомата: со стартовым состоянием и со стартовым состоянием соответственно. Нужно проверить их на эквивалентность.
Замечание: для реализации оба автомата обязательно должны иметь дьявольские состояния.
Проверка через минимизацию
Для этого построим автомат , содержащий все состояния обоих автоматов и изначальные переходы между ними. Стартовым состоянием в новом автомате можно сделать или — это не имеет значения. При этом состояния одного из автоматов станут недостижимыми из новый стартовой вершины в новом автомате, но для алгоритма это и не важно.
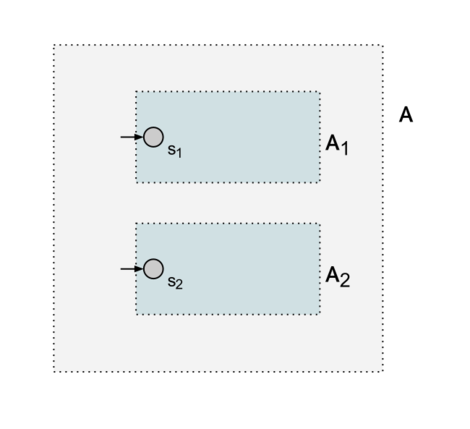
Осталось лишь проверить на эквивалентность состояния и в полученном автомате. Их эквивалентность совпадает с эквивалентностью автоматов и . Для этого можно применить алгоритм минимизации ДКА, который разбивает все состояния на классы эквивалентности. Если состояния и нового автомата в одном классе эквивалентности — исходные автоматы эквивалентны.
Также можно минимизировать каждый автомат отдельно и проверить минимизированные версии на изоморфизм.
Проверка через BFS
Два автомата можно также проверить на эквивалентность, используя обход в ширину. Будем синхронно обходить два автомата, начиная со стартовых состояний, в поисках такой строки, которая различает два состояний этих автоматов. То есть она будет допускаться одним автоматом, но не будет принадлежать языку другого.
Поскольку эквивалентные автоматы допускают один тот же язык, при переходе по одним и тем же символам в обоих автоматах, слово должно приниматься обоими автоматами одновременно. То есть вершины, в которые мы перешли, должны быть либо одновременно терминальными, либо одновременно нетерминальными, что и проверяет приведённый алгоритм.
Псевдокод
<wikitex>
// $\mathtt{aut}[i][c]$ — номер состояния, в которое есть переход из состояния $i$ по символу $c$
boolean $\mathtt{bfsEquivalenceCheck}$($\mathtt{aut1}$ : int[][], $\mathtt{aut2}$ : int[][]):
$Q.\mathtt{push}(\langle s_1, s_2 \rangle) $ // — очередь из пар состояний
$\mathtt{used1}[s_1] \leftarrow $ true
$\mathtt{used2}[s_2] \leftarrow $ true
while $Q \ne \varnothing $
$u, v \leftarrow Q.\mathtt{pop}()$
if $\mathtt{isTerminal1[u]} \ne \mathtt{isTerminal2[v]}$
return false
for $c \in \Sigma$
if not $\mathtt{used1[aut1}[u][c]]$ or not $\mathtt{used2[aut2}[v][c]]$
$Q.\mathtt{push}(\langle \mathtt{aut1}[u][c], \mathtt{aut2}[v][c] \rangle)$
$\mathtt{used1[aut1}[u][c]] \leftarrow $ true
$\mathtt{used2[aut2}[v][c]] \leftarrow $ true
return true
Корректность алгоритма следует из строго доказательства того факта, что если два состояния $u$ и $v$ различаются какой-то строкой, то они различаются строкой длины $O(n)$.
Интуитивное понимание алгоритма такое: пусть по строке $w$ мы пришли в состояния $ \langle u, v \rangle $, и пусть они оба нетерминальные. После этого совершим переход по символу $c$ в состояния $ \langle u', v' \rangle $.
Тогда если $\mathtt{isTerminal1[u']} \ne \mathtt{isTerminal2[v']}$, то строка $wc$ различает эти два состояния. А значит автоматы не эквивалентны. </wikitex>