Участник:Kabanov — различия между версиями
Kabanov (обсуждение | вклад) |
Kabanov (обсуждение | вклад) м |
||
| Строка 1: | Строка 1: | ||
| − | + | '''Триангуляция полигона ''' — декомпозиция многоугольника <tex>P</tex> на множество треугольников, внутренние области которых попарно не пересекаются и объединение которых в совокупности составляет <tex>P</tex>. В строгом смысле слова, вершины этих треугольников должны совпадать с вершинами исходного многоугольника. Триангуляция любого многоугольника не единственна. В этом можно убедиться из примера на рисунке. | |
| − | + | ||
| + | На плоскости задан произвольный многоугольник. Стороны многоугольника не пересекаются. Требуется найти его триангуляцию. | ||
| + | |||
| + | == Теорема о существовании триангуляции == | ||
| + | |||
| + | '''Простым многоугольником''' является фигура, ограниченная одной замкнутой ломаной, стороны которой не пересекаются. Таким образом, случаи многоугольников с дырками в теореме исключаются. | ||
| + | {{Теорема | ||
| + | |about = О существовании триангуляции многоугольника | ||
| + | |statement = | ||
| + | У любого простого <tex>n</tex>-вершинного многоугольника <tex>P</tex> всегда существует триангуляция, причём количество треугольников в ней <tex>n - 2</tex> независимо от самой триангуляции. | ||
| + | |proof= | ||
| + | [[Файл:Proof theorem.jpg|100px|thumb|right]] | ||
| + | Доказательство ведётся индуктивно по <tex>n</tex>. При <tex>n = 3</tex> теорема тривиальна. Рассмотрим случай при <tex>n > 3</tex> и предположим, что теорема выполняется при всех <tex>m < n</tex>. Докажем существование диагонали в многоугольнике <tex>P</tex>. Возьмём самую левую по оси <tex>x</tex> вершину <tex>v</tex> многоугольника <tex>P</tex> и две смежных с ней вершины <tex>u</tex> и <tex>w</tex>. Если отрезок <tex>uw</tex> принадлежит внутренней области <tex>P</tex> — мы нашли диагональ. В противном случае, во внутренней области треугольника <tex>\Delta uwv</tex> или на самом отрезке <tex>uw</tex> содержится одна или несколько вершин <tex>P</tex>. Выберем из них наиболее удалённую от <tex>uw</tex> вершину <tex>v'</tex>. Отрезок, соединяющий <tex>v</tex> и <tex>v'</tex> не может пересекать ребро <tex>P</tex>, поскольку в противном случае одна из вершин этого ребра будет располагаться дальше от <tex>uw</tex>, чем <tex>v'</tex>. Это противоречит условию выбора <tex>v'</tex>. В итоге получаем, что <tex>v'v</tex> — диагональ. | ||
| + | Любая диагональ делит <tex>P</tex> на два многоугольника <tex>P_1</tex> и <tex>P_2</tex>. За <tex>m_1</tex> и <tex>m_2</tex> обозначим количество вершин в <tex>P_1</tex> и <tex>P_2</tex> соответственно. <tex>m_1 < n</tex> и <tex>m_2 < n</tex>, поэтому по предположению индукции у <tex>P_1</tex> и <tex>P_2</tex> существует триангуляция, следовательно и у <tex>P</tex> она существует. | ||
| + | |||
| + | Докажем, что триангуляция <tex>P</tex> состоит из <tex>n - 2</tex> треугольников. Рассмотрим произвольную диагональ <tex>d</tex> в триангуляции <tex>T_P</tex>. <tex>d</tex> делит <tex>P</tex> на два многоугольника <tex>P_1</tex> и <tex>P_2</tex>, количество вершин в которых <tex>m_1</tex> и <tex>m_2</tex> соответственно. Каждая вершина <tex>P</tex> встречается только в одном из двух многоугольников <tex>P_1</tex> и <tex>P_2</tex>, за исключением тех, которые являются концами <tex>d</tex>, поэтому справедливо следующее: <tex>m_1 + m_2 = n + 2</tex>. По индукции, любая триангуляция <tex>P_i</tex> состоит из <tex>m_i - 2</tex> треугольников, откуда следует, что <tex>T_P</tex>. состоит из <tex>(m_1 - 2) + (m_2 - 2) = n - 2</tex> треугольников. | ||
| + | }} | ||
| + | |||
| + | == Ушной метод == | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | Вершина <tex>v_i</tex> называется '''ухом''', если диагональ <tex>v_{i-1}v_{i+1}</tex> лежит строго во внутренней области многоугольника <tex>P</tex> | ||
| + | }} | ||
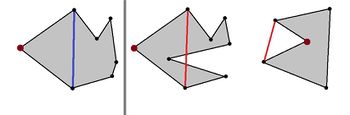
| + | [[Файл:Ear1.jpg|350px|thumb|left|В первом случае выделенная вершина является ухом, в остальных нет]] | ||
| + | |||
| + | {{Теорема | ||
| + | |about = О существовании двух ушей многоугольника | ||
| + | |statement = | ||
| + | У любого простого <tex>n</tex>-вершинного многоугольника <tex>P</tex> всегда существует два не пересекающихся между собой уха. | ||
| + | |proof= | ||
| + | [[Файл:Ear case1.jpg|200px|thumb|left]] | ||
| + | [[Файл:Ear_case2.jpg|200px|thumb|right]] | ||
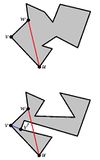
| + | Доказательство будем вести по индукции. Базовый случай: <tex>n = 4</tex>. Предположим для всех многоугольников, количество вершин в которых не больше <tex>n</tex>, теорема верна. Рассмотрим многоугольник <tex>P</tex>, в котором <tex>n+1</tex> вершина. Далее возможны два случая: | ||
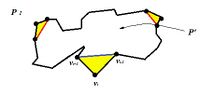
| + | * Произвольная выпуклая вершина <tex>v_i</tex> многоугольника <tex>P</tex> является ухом. Отрезав это ухо, мы уменьшим число вершин <tex>P</tex> на одну. В результате, получиv <tex>n</tex>-вершинный многоугольник <tex>P'</tex>. По предположению индукции у него существует два непересекающихся уха. Учитывая, что уши <tex>P'</tex> являются ушами и <tex>P</tex>, несложно заметить, что для <tex>P</tex> теорема верна. | ||
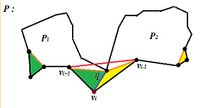
| + | * Произвольная выпуклая вершина <tex>v_i</tex> многоугольника <tex>P</tex> не является ухом. В таком случае в треугольнике <tex>\Delta v_{i-1}v_{i}v_{i+1}</tex> лежат вершины, принадлежащие <tex>P</tex>. Из этих вершин выберем вершину <tex>q</tex>, которая будет ближе всего к <tex>v_i</tex>. Проведём отрезок <tex>Q</tex>, который разделит <tex>P</tex> на два многоугольника: <tex>P_1</tex> и <tex>P_2</tex>. В каждом из них будет не более <tex>n</tex> вершин, следовательно у каждого будет по два непересекающихся уха. Даже если предположить, что ухо из <tex>P_1</tex> и ухо из <tex>P_2</tex> будут пересекаться по стороне <tex>v_{i}q</tex>, в <tex>P</tex> всё равно будет не менее двух непересекающихся ушей. | ||
| + | }} | ||
| + | |||
| + | ==== Идея ==== | ||
| + | Рассмотрим все вершины многоугольника <tex>P</tex>, и где возможно, будем отрезать уши до тех пор, пока <tex>P</tex> не станет треугольником. | ||
| + | |||
| + | Будем рассматривать вершины многоугольника в порядке обхода. Индексирование вершин для удобства будем вести по модулю <tex>n</tex>, т.е. <tex>v_{-1} = v_{n-1}</tex> и <tex>v_0 = v_n</tex>. Если вершина <tex>v_i</tex> является ухом, построим диагональ <tex>v_{i+1}v_{i-1}</tex> и отрежем треугольник <tex>\Delta v_{i-1}v_{i}v_{i+1}</tex> от <tex>P</tex>. В противном случае переходим к следующей вершине <tex>v_{i+1}</tex> в порядке обхода. | ||
| + | |||
| + | ==== Алгоритм ==== | ||
| + | При проверке каждой вершину следует для начала проверить, является ли она выпуклой, в противном случае её просто нет надобности рассматривать в качестве уха. Это несложно сделать, воспользовавшись [[Предикат_"левый_поворот"|левым поворотом]]. "Ушную" проверку вершины будем осуществлять алгоритмом принадлежности точки <tex>n</tex>-угольнику (в нашем случае треугольнику). В качестве поддерживаемых структур удобно хранить DCEL, в котором будем строить новые диагонали, и список вершин с двойными связями, аналогичный DCEL по построению. | ||
| + | |||
| + | ==== Псевдокод ==== | ||
| + | DCVL D1 //список вершин doubly connected vertex list по аналогии с DCEL | ||
| + | DCEL D2 | ||
| + | Construct(D1); | ||
| + | Construct(D2); | ||
| + | vertex v = random_vertex_of(D1); | ||
| + | while size_of(D1) <tex> \neq </tex> 3 | ||
| + | if IsConvex(v) //проверка на выпуклость | ||
| + | for each Vertex v_i in D1 | ||
| + | if v_i <tex> \neq </tex> v, v.prev(), v.next() //проверка всех вершин на | ||
| + | and v_i <tex>\in </tex> Triangle(v, v.prev(), v.next())//принадлежность треугольнику, | ||
| + | //одной из вершин которого | ||
| + | //является потенциальное ухо v. | ||
| + | edge e = new edge(v.prev, v.next) | ||
| + | Insert e in D2; | ||
| + | v = v.next | ||
| + | Delete v.prev from D1 | ||
| + | |||
| + | ==== Корректность ==== | ||
| + | При нахождении каждого уха от многоугольника <tex>P</tex> отрезается треугольник, состоящий из самого уха и его двух смежных вершин. Существование ушей в свою очередь следует из теоремы, доказанной выше. В конце алгоритма, когда все уши от <tex>P</tex> отрезаны, остается только один треугольник. Как несложно видеть, триангуляция выстраивается корректно. | ||
| + | |||
| + | ==== Оценка работы ==== | ||
| + | Изначально в многоугольнике содержится <tex>\mathcal{O}(n)</tex> ушей. Нетрудно понять, что в процессе отрезания ушей, смежные точки могут тоже становиться ушами. В результате триангуляции образуется <tex>n - 3</tex> диагонали, соответственно максимальное количество вершин, которые в процессе могут становиться ушами <tex>2n - 6</tex>. Итого общее количество ушей будет <tex>\mathcal{O}(n)</tex>. Определить, является ли вершина ухом можно за <tex>\mathcal{O}(n)</tex>, поскольку используется алгоритм определения принадлежности точки треугольнику — это <tex>\mathcal{O}(1)</tex>. Таким образом общий процесс отрезания ушей займёт <tex>\mathcal{O}(n^2)</tex>. Невыпуклых вершин всего <tex>\mathcal{O}(n)</tex>, каждая из них обрабатывается за константу, поэтому общее время для их обработки <tex>\mathcal{O}(n)</tex>. Списки рёбер и вершин строятся за линейное время, добавление ребра и удаление вершины в каждом из них работает за константу. Общее время <tex>\mathcal{O}(n^2)</tex>. Поскольку храним только два списка — память линейная. | ||
| + | |||
| + | [[Категория: Вычислительная геометрия]] | ||
Версия 21:31, 20 января 2015
Триангуляция полигона — декомпозиция многоугольника на множество треугольников, внутренние области которых попарно не пересекаются и объединение которых в совокупности составляет . В строгом смысле слова, вершины этих треугольников должны совпадать с вершинами исходного многоугольника. Триангуляция любого многоугольника не единственна. В этом можно убедиться из примера на рисунке.
На плоскости задан произвольный многоугольник. Стороны многоугольника не пересекаются. Требуется найти его триангуляцию.
Содержание
Теорема о существовании триангуляции
Простым многоугольником является фигура, ограниченная одной замкнутой ломаной, стороны которой не пересекаются. Таким образом, случаи многоугольников с дырками в теореме исключаются.
| Теорема (О существовании триангуляции многоугольника): |
У любого простого -вершинного многоугольника всегда существует триангуляция, причём количество треугольников в ней независимо от самой триангуляции. |
| Доказательство: |
|
Доказательство ведётся индуктивно по . При теорема тривиальна. Рассмотрим случай при и предположим, что теорема выполняется при всех . Докажем существование диагонали в многоугольнике . Возьмём самую левую по оси вершину многоугольника и две смежных с ней вершины и . Если отрезок принадлежит внутренней области — мы нашли диагональ. В противном случае, во внутренней области треугольника или на самом отрезке содержится одна или несколько вершин . Выберем из них наиболее удалённую от вершину . Отрезок, соединяющий и не может пересекать ребро , поскольку в противном случае одна из вершин этого ребра будет располагаться дальше от , чем . Это противоречит условию выбора . В итоге получаем, что — диагональ. Любая диагональ делит на два многоугольника и . За и обозначим количество вершин в и соответственно. и , поэтому по предположению индукции у и существует триангуляция, следовательно и у она существует. Докажем, что триангуляция состоит из треугольников. Рассмотрим произвольную диагональ в триангуляции . делит на два многоугольника и , количество вершин в которых и соответственно. Каждая вершина встречается только в одном из двух многоугольников и , за исключением тех, которые являются концами , поэтому справедливо следующее: . По индукции, любая триангуляция состоит из треугольников, откуда следует, что . состоит из треугольников. |
Ушной метод
| Определение: |
| Вершина называется ухом, если диагональ лежит строго во внутренней области многоугольника |
| Теорема (О существовании двух ушей многоугольника): |
У любого простого -вершинного многоугольника всегда существует два не пересекающихся между собой уха. |
| Доказательство: |
|
Доказательство будем вести по индукции. Базовый случай: . Предположим для всех многоугольников, количество вершин в которых не больше , теорема верна. Рассмотрим многоугольник , в котором вершина. Далее возможны два случая:
|
Идея
Рассмотрим все вершины многоугольника , и где возможно, будем отрезать уши до тех пор, пока не станет треугольником.
Будем рассматривать вершины многоугольника в порядке обхода. Индексирование вершин для удобства будем вести по модулю , т.е. и . Если вершина является ухом, построим диагональ и отрежем треугольник от . В противном случае переходим к следующей вершине в порядке обхода.
Алгоритм
При проверке каждой вершину следует для начала проверить, является ли она выпуклой, в противном случае её просто нет надобности рассматривать в качестве уха. Это несложно сделать, воспользовавшись левым поворотом. "Ушную" проверку вершины будем осуществлять алгоритмом принадлежности точки -угольнику (в нашем случае треугольнику). В качестве поддерживаемых структур удобно хранить DCEL, в котором будем строить новые диагонали, и список вершин с двойными связями, аналогичный DCEL по построению.
Псевдокод
DCVL D1 //список вершин doubly connected vertex list по аналогии с DCEL DCEL D2 Construct(D1); Construct(D2); vertex v = random_vertex_of(D1); while size_of(D1) 3 if IsConvex(v) //проверка на выпуклость for each Vertex v_i in D1 if v_i v, v.prev(), v.next() //проверка всех вершин на and v_i Triangle(v, v.prev(), v.next())//принадлежность треугольнику, //одной из вершин которого //является потенциальное ухо v. edge e = new edge(v.prev, v.next) Insert e in D2; v = v.next Delete v.prev from D1
Корректность
При нахождении каждого уха от многоугольника отрезается треугольник, состоящий из самого уха и его двух смежных вершин. Существование ушей в свою очередь следует из теоремы, доказанной выше. В конце алгоритма, когда все уши от отрезаны, остается только один треугольник. Как несложно видеть, триангуляция выстраивается корректно.
Оценка работы
Изначально в многоугольнике содержится ушей. Нетрудно понять, что в процессе отрезания ушей, смежные точки могут тоже становиться ушами. В результате триангуляции образуется диагонали, соответственно максимальное количество вершин, которые в процессе могут становиться ушами . Итого общее количество ушей будет . Определить, является ли вершина ухом можно за , поскольку используется алгоритм определения принадлежности точки треугольнику — это . Таким образом общий процесс отрезания ушей займёт . Невыпуклых вершин всего , каждая из них обрабатывается за константу, поэтому общее время для их обработки . Списки рёбер и вершин строятся за линейное время, добавление ребра и удаление вершины в каждом из них работает за константу. Общее время . Поскольку храним только два списка — память линейная.