Суффиксный массив — различия между версиями
KK (обсуждение | вклад) (→См. также) |
Shersh (обсуждение | вклад) м (→Применения) |
||
| Строка 11: | Строка 11: | ||
== Применения == | == Применения == | ||
| − | * Позволяет найти все вхождения образца <tex>p</tex> в строку <tex>s</tex> за время <tex>O(|p| + \log(|s|))</tex> | + | * Позволяет найти все вхождения образца <tex>p</tex> в строку <tex>s</tex> за время <tex>O(|p| + \log(|s|))</tex>. |
* Позволяет вычислить наибольший общий префикс (англ. ''longest common prefix'', ''LCP'') для всех соседних в лексикографическом порядке суффиксов строки <tex>s</tex> за <tex>O(|s|)</tex>, то есть построить массив <tex>LCP[1 .. |s| - 1]</tex>, где <tex>LCP[i]</tex> {{---}} длина наибольшего общего префикса суффиксов <tex>s[suf[i] .. |s|]</tex> и <tex>s[suf[i + 1] .. |s|]</tex>. | * Позволяет вычислить наибольший общий префикс (англ. ''longest common prefix'', ''LCP'') для всех соседних в лексикографическом порядке суффиксов строки <tex>s</tex> за <tex>O(|s|)</tex>, то есть построить массив <tex>LCP[1 .. |s| - 1]</tex>, где <tex>LCP[i]</tex> {{---}} длина наибольшего общего префикса суффиксов <tex>s[suf[i] .. |s|]</tex> и <tex>s[suf[i + 1] .. |s|]</tex>. | ||
* Позволяет найти количество различных подстрок в строке за время <tex>O(|s| \log(|s|))</tex> и <tex>O(|s|)</tex> дополнительной памяти. | * Позволяет найти количество различных подстрок в строке за время <tex>O(|s| \log(|s|))</tex> и <tex>O(|s|)</tex> дополнительной памяти. | ||
Версия 23:06, 13 апреля 2015
| Определение: |
| Cуффиксным массивом (англ. suffix array) строки называется массив целых чисел от до , такой, что суффикс — -й в лексикографическом порядке среди всех непустых суффиксов строки . |
Содержание
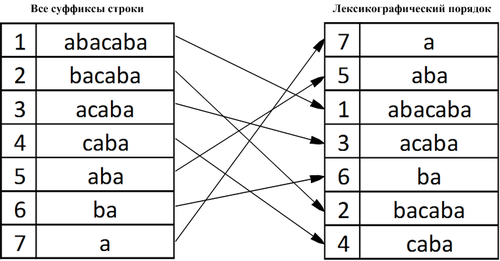
Пример
Значит, суффиксный массив для строки равен .
Применения
- Позволяет найти все вхождения образца в строку за время .
- Позволяет вычислить наибольший общий префикс (англ. longest common prefix, LCP) для всех соседних в лексикографическом порядке суффиксов строки за , то есть построить массив , где — длина наибольшего общего префикса суффиксов и .
- Позволяет найти количество различных подстрок в строке за время и дополнительной памяти.
- Позволяет найти наименьший циклический сдвиг строки за время .
См. также
- Построение суффиксного массива с помощью стандартных методов сортировки
- Алгоритм поиска подстроки в строке с помощью суффиксного массива
- Алгоритм Касаи и др.
Источники
- Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.
- MAXimal :: algo :: Суффиксный массив
- Википедия — Суффиксный массив
- Wikipedia — Suffix array
- Habrahabr — Суффиксный массив — удобная замена суффиксного дерева