Сжатое суффиксное дерево — различия между версиями
Mogikan (обсуждение | вклад) (→Поиск строки максимальной длины, ветвящейся влево и вправо) |
(→Поиск строки максимальной длины, ветвящейся влево и вправо v 1.0) |
||
| Строка 181: | Строка 181: | ||
}} | }} | ||
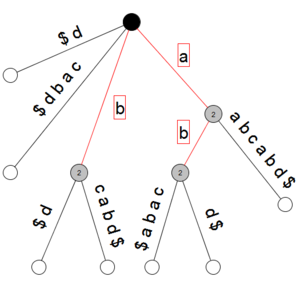
[[Файл:RightMergingSS.png|thumb|right|Суффиксное дерево для строки <tex>aabcabd</tex>]] | [[Файл:RightMergingSS.png|thumb|right|Суффиксное дерево для строки <tex>aabcabd</tex>]] | ||
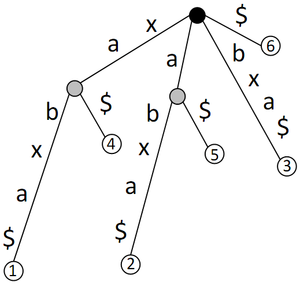
| − | + | Первая часть алгоритма: построим Суффиксное дерево при помощи [[Алгоритм Укконена|Алгоритма Укконена]]. При создании ответвления будем увеличивать счётчик вершины, от которой идёт новый лист, на 1, если его пометка <tex>\ne</tex> <tex>\$</tex>. Таким образом, если у вершины счётчик <tex>></tex> 1, то подстрока, которую мы восстановим, идя вверх по дереву до корня, будет ветвящейся вправо (в примере для строки <tex>aabcabd</tex> это <tex>b</tex>, <tex>a</tex> и <tex>ab</tex>). Далее введём термины ''левый символ'' и ''вершина различная влево'', что бы найти строки, ветвящиеся влево. | |
| − | + | {{Определение | |
| − | + | |definition= | |
| − | + | '''Левый символ''' для позиции <tex>i</tex> строки <tex>S</tex> - это символ <tex>S(i-1)</tex>. | |
| + | '''Левым символом''' листа <tex>L</tex> называется левый символ начала суффикса, представляемого этим листом. | ||
| + | }} | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | '''Вершина <tex>v</tex> различна влево''', если как минимум два листа в поддереве <tex>v</tex> имеют различные ''левые символы''. По определению лист не может быть различным влево. | ||
| + | }} | ||
{{Теорема | {{Теорема | ||
|about= | |about= | ||
| − | + | о строке, ветвящейся вправо и влево | |
|statement= | |statement= | ||
| − | + | Строка <tex>a</tex>, соответствующая пути к вершине <tex>v</tex>, является ветвящейся вправо и влево тогда и только тогда, когда вершина <tex>v</tex> ''различна влево'' и счётчик вершины <tex>></tex> 1. | |
| − | |||
| − | |||
| − | |||
|proof= | |proof= | ||
| + | <tex>\Leftarrow</tex> | ||
| + | *Предположим, что <tex>v</tex> различна влево. Значит, что существуют подстроки <tex>cs</tex> и <tex>ds</tex>. | ||
| + | *Пусть за первой подстрокой следует символ <tex>p</tex>. Если за второй подстрокой следует символ, <tex>\ne p</tex>, то <tex>s</tex> - строка, ветвящаяся вправо и влево. | ||
| + | *Так как у <tex>v</tex> есть два различных ребёнка, которые начинаются с различных символов <tex>p,q \ne \$</tex>, строка является ветвящейся вправо. | ||
| + | |||
| + | <tex>\Rightarrow</tex> | ||
| + | *Пусть строка <tex>s</tex> является ветвящейся вправо и влево. | ||
| + | *Тогда существуют подстроки <tex>csa</tex> и <tex>dsb</tex>. | ||
| + | *В суффиксном дереве существует вершина <tex>v</tex> соответствующая строке <tex>s</tex> (так как есть как минимум два суффикса, начинающиеся со строки <tex>s</tex>). | ||
| + | *У вершины <tex>v</tex>, есть как минимум два ребёнка, которые начинаются с символов <tex>a</tex> и <tex>b</tex> <tex>\Rightarrow</tex> счётчик вершины <tex>></tex> 2. | ||
| + | *Так же у вершины <tex>v</tex>, есть как минимум два ребёнка, у которых ''левый символ'' <tex>c</tex> и <tex>d</tex>, значит вершина <tex>v</tex> ''различна влево'' по определению. | ||
}} | }} | ||
| + | |||
| + | Будем хранить в вершинах суффиксного дерева следующую информацию: левый символ или флаг, означающий, что вершина различна влево. | ||
| + | Вторая часть алгоритма начинает с листов суффиксного дерева, записывая для них левый символ. Затем мы обрабатываем вершины снизу вверх. При обработке вершины <tex>v</tex> проверяются её дети, если хотя бы один из них различен влево, то записываем, что вершина <tex>v</tex> различна влево. | ||
| + | Если никто из детей не различен влево, то проверяем их символы, привязанные к вершинам детей. | ||
| + | Если все символы равны <tex>x</tex>, то запишем в <tex>v x</tex>, иначе запишем в <tex>v</tex>, что она различна влево. | ||
| + | Так как время проверки детей <tex>v</tex> пропорционально числу детей, время работы всего алгоритма - <tex>O(n)</tex>. | ||
| + | |||
| + | Далее соберём все строки удовлетворяющие условию теоремы и найдём среди них максимальную (так же этот алгоритм можно использовать для нахождения количества строк, ветвящихся влево и вправо). | ||
| + | |||
| + | Таким образом мы умеем искать строку максимальной длины, ветвящуюся влево и вправо за <tex>ST+O(N)</tex>. | ||
==См. также== | ==См. также== | ||
Версия 21:01, 21 мая 2015
Суффиксный бор — удобная структура данных для поиска подстроки в строке, но она требует порядка квадрата длины исходной строки памяти. Оптимизацией суффиксного бора, требующей линейное количество памяти, является сжатое суффиксное дерево рассматриваемое далее.
Содержание
Определение
| Определение: |
Суффиксное дерево (сжатое суффиксное дерево) для строки (где ) — дерево с листьями, обладающее следующими свойствами:
|
Данное определение порождает следующую проблему:
Рассмотрим дерево для строки : суффикс является префиксом суффикса , а, значит, этот суффикс не закачивается в листе. Для решения проблемы в конце строки добавляют символ, не входящий в исходный алфавит: защитный символ. Обозначим его как . Любой суффикс строки с защитным символом действительно заканчивается в листе и только в листе, т. к. в такой строке не существует двух различных подстрок одинаковой длины, заканчивающихся на .
Далее — длина строки с защитным символом.
Количество вершин
По определению, в суффиксном дереве содержится листьев. Оценим количество внутренних вершин такого дерева.
| Лемма: |
Количество внутренних вершин дерева, каждая из которых имеет не менее двух детей, меньше количества листьев. |
| Доказательство: |
|
Докажем лемму индукцией по количеству листьев . База При в дереве одна внутренняя вершина, следовательно утверждение верно. Переход Возьмем вершину в дереве с листами, у которой два ребенка — листья. Рассмотрим возможные случаи: 1) У нее более двух детей. Тогда отрежем от нее лист. Получим дерево с листьями, причем в нем количество внутренних вершин такое же, как в исходном дереве. Но у полученного дерева по индукционному предположению менее внутренних вершин, а, значит, и для исходного дерева лемма верна. 2) У нее ровно два ребенка. Отрежем их, получим дерево с листьями, количество внутренних вершин которого на меньше, чем в исходном дереве. Тогда по индукционному предположению у него менее внутренних вершин, значит, в исходном дереве их меньше . |
Занимаемая память
Представим дерево как двумерный массив размера , где — количество вершин в дереве, — мощность алфавита. Для любого суффиксного дерева верна предыдущая лемма (у каждой вершины, по определению, не менее двух детей), значит, . Каждая ячейка содержит информацию о том, в какую вершину ведет ребро из -ой вершины по -ому символу и индексы начала и конца подстроки, записанной на данном переходе. Итак, дерево занимает памяти.
Построение суффиксного дерева
Наивный алгоритм
Рассмотрим наивный алгоритм построения суффиксного дерева строки :
go[0] = Vertex() // корень
count = 0 // номер последней вершины, созданной в дереве (глобальная переменная)
for i = 0 to n // для каждого символа строки
insert(i, n) // добавляем суффикс, начинающийся с него
insert(l, r):
cur = 0
while l < r
if go[cur][s[l]].v == -1 // если мы не можем пойти из вершины по символу
createVertex(cur, l, r) // создаем новую вершину
else
start = go[cur][s[l]].l
finish = go[cur][s[l]].r
hasCut = false
for j = start to finish // для каждого символа на ребре из текущей вершины
if s[l+j-start] s[j] // если нашли не совпадающий символ
// создаем вершину на ребре
old = go[cur][s[l]]
createVertex(cur, l, j - 1)
go[count][s[j]].v = old
go[count][s[j]].r = j
go[count][s[j]].l = finish
createVertex(count, l + j - start, r)
hasCut = true
break
if !hasCut
cur = go[cur][s[l]].v // переходим по ребру
l = l + finish - start // двигаемся по суффиксу на длину подстроки, записанной на ребре
else
break
createVertex(cur, l, r):
go[++count] = Vertex()
go[cur][s[l]].v = count
go[cur][s[l]].l = l
go[cur][s[l]].r = r
Этот алгоритм работает за время , однако алгоритм Укконена позволяет построить сжатое суффиксное дерево за .
Построение из суффиксного массива
Пусть нам известен суффиксный массив строки , его можно получить алгоритмом Карккайнена-Сандерса за линейное время. Для преобразования нам также понадобится массив (longest common prefix), который можно получить алгоритмом Касаи.
В этом преобразовании используется тот же инвариант, что и в других суффиксных структурах:
- Строка заканчивается специальным символом, который больше не встречается в строке.
- Следствие: , где — длина суффикса, соответствующего .
Будем строить дерево, добавляя суффиксы в лексикографическом порядке. Чтобы ускорить добавление, будем использовать то, что -ый суффикс имеет с предыдущим общих символов. Тогда добавление из корня не отличается от того, что мы поднимемся вверх из предыдущего суффикса до глубины и продолжим построение оттуда. Инвариант позволяет нам утверждать, что ни один лист мы не сможем продолжить, и нам всегда нужно будет хоть раз подняться из него вверх. Поскольку суффиксы отсортированы лексикографически, мы не будем спускаться по ребру после того, как уже поднялись из него из-за несовпадения символа. Все это позволяет сформулировать алгоритм добавления суффикса по известной вершине предыдущего суффикса:
- Подняться из вершины вверх до глубины
- Если эта глубина находится на ребре, разрезать ребро по ней.
- Вставить новую вершину как сына вершины с глубиной
В вершинах дерева мы будем хранить предка , стек детей в лексикографическом порядке ребер , глубину вершины в символах от корня .
Соответственно, конструктор вершины имеет вид Node(Node parent, int depth).
Node addNextSuffix(Node previous, int length, int lcp):
if previous.depth == 0 or previous.depth == lcp // Добавляем к сыновьям текущей вершины
added = Node(previous, length)
previous.children.push(added)
return added
else
if previous.parent.depth < lcp: // Нужно разрезать ребро
inserted = Node(prevous.parent, lcp)
previous.parent.children.pop()
previous.parent.children.push(inserted)
inserted.children.push(previous)
previous.parent = inserted
return addNextSuffix(previous.parent, length, lcp)
Node buildSuffixTree(int[] suf, int[] lcp, int length):
root = Node(null, 0)
previous = root
for i = 1 to length
previous = addNextSuffix(previous, length - suf[i], lcp[i])
return root
В процессе построения мы нигде не запоминали сами позиции строки, соответствующие ребрам. Чтобы их восстановить, достаточно определить максимальный суффикс, который проходит по этому ребру. Для этого с помощью обхода в глубину посчитаем для каждой вершину дерева максимальную глубину ее листа .
Тогда ребро определяется так:
function calculatePositions(Node parent, Node child, int stringLength): start = stringLength - child.maxDepth + parent.depth end = start + child.depth - parent.depth - 1
Для асимптотического анализа будем использовать в качестве потенциала глубину в вершинах. При добавлении суффикса мы спускаемся один раз, подняться выше корня мы не можем, значит, и подниматься мы будем суммарно раз. Обход в глубину также выполняется за , итоговая асимптотика .
Использование сжатого суффиксного дерева
Суффиксное дерево позволяет за линейное время найти:
- Количество различных подстрок данной строки
- Наибольшую общую подстроку двух строк
- Суффиксный массив и массив (longest common prefix) исходной строки
- Строку максимальной длины, ветвящуюся влево и вправо за
Построение суффиксного массива и массива lcp из суффиксного дерева
Пусть к строке дописан специальный символ для сохранения инварианта. Рассмотрим лексикографический по ребрам порядок обхода сжатого суффиксного дерева. Пусть два суффикса имеют общее начало, но различаются в -ом символе. Первым будет рассмотрено поддерево по ребру с меньшим символом, значит и лист, соответствующий этому суффиксу, будет посещен первым.
Тогда суффиксный массив строится из суффиксного дерева обходом в глубину в указанном порядке. Пусть длина строки , глубина листа в символах , тогда номер суффикса .
Для заполнения массива нам понадобится вершина , которая будет означать вершину с минимальной глубиной, в которую мы поднимались при переходе между суффиксами. Поскольку мы точно поднимались туда, но не поднимались выше, это будет наименьший общий предок этих узлов. Из этого следует, что у рассматриваемых суффиксов совпадает ровно символов.
int curPos = 0
Node minNode = root
// Для заполнения нужно вызвать dfs(root)
function dfs(Node n):
if n.children.size == 0
suf[curPos] = length - n.depth
lcp[curPos] = minNode.depth
curPos++
minNode = n
else
foreach child in n.children
if n.depth < minNode.depth:
minNode = n
dfs(child)
Асимптотика алгоритма совпадает с асимптотикой обхода в глубину и составляет .
Таким образом, мы умеем за строить суффиксное дерево, суффиксный массив и преобразовывать одно в другое.
Поиск строки максимальной длины, ветвящейся влево и вправо
| Определение: |
| Строка называется ветвящейся вправо в , если существуют символы и , такие что : и - подстроки . Аналогично, ветвящаяся влево, если и - подстроки . |
Первая часть алгоритма: построим Суффиксное дерево при помощи Алгоритма Укконена. При создании ответвления будем увеличивать счётчик вершины, от которой идёт новый лист, на 1, если его пометка . Таким образом, если у вершины счётчик 1, то подстрока, которую мы восстановим, идя вверх по дереву до корня, будет ветвящейся вправо (в примере для строки это , и ). Далее введём термины левый символ и вершина различная влево, что бы найти строки, ветвящиеся влево.
| Определение: |
| Левый символ для позиции строки - это символ . Левым символом листа называется левый символ начала суффикса, представляемого этим листом. |
| Определение: |
| Вершина различна влево, если как минимум два листа в поддереве имеют различные левые символы. По определению лист не может быть различным влево. |
| Теорема (о строке, ветвящейся вправо и влево): |
Строка , соответствующая пути к вершине , является ветвящейся вправо и влево тогда и только тогда, когда вершина различна влево и счётчик вершины 1. |
| Доказательство: |
|
|
Будем хранить в вершинах суффиксного дерева следующую информацию: левый символ или флаг, означающий, что вершина различна влево. Вторая часть алгоритма начинает с листов суффиксного дерева, записывая для них левый символ. Затем мы обрабатываем вершины снизу вверх. При обработке вершины проверяются её дети, если хотя бы один из них различен влево, то записываем, что вершина различна влево. Если никто из детей не различен влево, то проверяем их символы, привязанные к вершинам детей. Если все символы равны , то запишем в , иначе запишем в , что она различна влево. Так как время проверки детей пропорционально числу детей, время работы всего алгоритма - .
Далее соберём все строки удовлетворяющие условию теоремы и найдём среди них максимальную (так же этот алгоритм можно использовать для нахождения количества строк, ветвящихся влево и вправо).
Таким образом мы умеем искать строку максимальной длины, ветвящуюся влево и вправо за .
См. также
Источники информации
- Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.