Совершенное паросочетание в кубическом графе — различия между версиями
Profick (обсуждение | вклад) (Новая страница: «{{Теорема |id=th1. |author=Петерсон |statement=Кубический граф, у которого нет совершенного паросоче...») |
Profick (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
|id=th1. | |id=th1. | ||
|author=Петерсон | |author=Петерсон | ||
| − | |statement=Кубический граф, у которого нет совершенного паросочетания, содержит как минимум 3 моста. }} | + | |statement=Кубический граф, у которого нет совершенного паросочетания, содержит как минимум <tex>3</tex> моста. }} |
==Следствие теоремы Петерсона== | ==Следствие теоремы Петерсона== | ||
| Строка 21: | Строка 21: | ||
* компонента <tex>B</tex> соединена с <tex>E</tex> и компонента <tex>E</tex> соединена с <tex>F</tex> | * компонента <tex>B</tex> соединена с <tex>E</tex> и компонента <tex>E</tex> соединена с <tex>F</tex> | ||
* компонента <tex>A</tex> соединена с <tex>B</tex> и компонента <tex>E</tex> соединена с <tex>F</tex> | * компонента <tex>A</tex> соединена с <tex>B</tex> и компонента <tex>E</tex> соединена с <tex>F</tex> | ||
| − | Во всех трёх случаях если <tex>G(V - {c, d})</tex> расширить рёбрами <tex>(a, f), (b, e)</tex> (получим граф <tex>G'</tex>), добавленные рёбра будут лежать на некотором цикле в <tex>G'</tex> (рисунок <tex>4</tex>). Так же, для любой пары вершин <tex>u, v</tex> <math>\in</math> | + | Во всех трёх случаях если <tex>G(V - {c, d})</tex> расширить рёбрами <tex>(a, f), (b, e)</tex> (получим граф <tex>G'</tex>), добавленные рёбра будут лежать на некотором цикле в <tex>G'</tex> (рисунок <tex>4</tex>). Так же, для любой пары вершин <tex>u, v</tex> <math>\in</math> <tex>{a, b, e, f}</tex> существует цикл в <tex>G'</tex>, содержащий данные вершины. Чтобы доказать, что <tex>G'</tex> двусвязен, нужно показать, что каждое ребро <tex>r</tex> из <tex>G'</tex> лежит на некотором цикле в <tex>G'</tex>. Пусть цикл <tex>C</tex> в <tex>G</tex> содержит <tex>r</tex> (такой цикл существует, так как <tex>G</tex> двусвязен). Если <tex>C</tex> не проходит через вершины <tex>c, d</tex> тогда <tex>C</tex> так же является циклом в <tex>G'</tex>, иначе построим цикл <tex>C'</tex> графа <tex>G'</tex> из <tex>C</tex> следующим образом: |
}} | }} | ||
Версия 16:02, 28 января 2016
| Теорема (Петерсон): |
Кубический граф, у которого нет совершенного паросочетания, содержит как минимум моста. |
Следствие теоремы Петерсона
Для любого двусвязного кубического графа существует совершенное паросочетание.
| Теорема (Фринк): |
Пусть — двусвязный кубический граф.
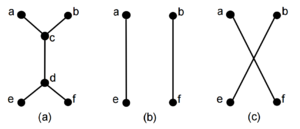
Возьмём ребро . Пусть вершины и смежены с вершиной , а вершины и смежны с вершиной (рисунок ). Как минимум одно из двух сокращений графа , состоящее из удаления вершин и пересоединения вершин рёбрами или (рисунок ) сохранит двусвязность графа. |
| Доказательство: |
|
Обозначим компоненты графа как , которые содержат вершины соответственно. Так как не имеет мостов (соответственно не является мостом) должно существовать ребро, соединяющее одну из компонент или , с одной из компонент или . Без потери общности предположим, что соединено с . Заметим, что рёбра так же не являются мостами, значит возможны три случая (с учётом изоморфизма) (рисунок ):
|
Алгоритм поиска совершенного паросочетания за (Frink's algorithm)
Главная идея алгоритма заключается в предыдущей теореме.