Rake-Compress деревья — различия между версиями
| Строка 16: | Строка 16: | ||
Входными данными для алгоритма Rake-Compress является лес корневых деревьев. К нему поочередно применяются операции <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> до тех пор, пока существует хотя бы одна живая вершина.<br>Во время каждой из этих операций выбирается некоторое множество попарно несмежных вершин, которое сжимается к своим родителям. После каждой операции лес сохраняется в специальном виде, что в дальнейшем дает возможность отвечать на запросы о структуре леса.<br> | Входными данными для алгоритма Rake-Compress является лес корневых деревьев. К нему поочередно применяются операции <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> до тех пор, пока существует хотя бы одна живая вершина.<br>Во время каждой из этих операций выбирается некоторое множество попарно несмежных вершин, которое сжимается к своим родителям. После каждой операции лес сохраняется в специальном виде, что в дальнейшем дает возможность отвечать на запросы о структуре леса.<br> | ||
Современная реализация Rake-Compress деревьев была предложена Р. А. Тарьяном и Р. Ф. Вернеком. | Современная реализация Rake-Compress деревьев была предложена Р. А. Тарьяном и Р. Ф. Вернеком. | ||
| + | |||
| + | Рассмотрим, как изменяется количество вершин в дереве после применения к нему операций <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex>. Разобьём все вершины дерева на три группы: входящая степень которых равна нулю, одному и больше одного. Обозначим их количество за <tex>T_0, T_1</tex> и <tex>T_2</tex> соответственно. | ||
| + | {{Лемма | ||
| + | |about=1 | ||
| + | |statement=<tex>T_2 \leqslant T_0 - 1</tex>. | ||
| + | |proof=Докажем по индукции по высоте дерева.<br>Для дерева из одной вершины утверждение верно.<br>Пусть утверждение доказано для деревьев высоты меньше <tex>h</tex>. Докажем для дерева высоты ровно <tex>h</tex>. Рассмотрим степень корня. Если корень имеет ровно одного ребенка, то переходим к случаю дерева высоты <tex>h - 1</tex>. Если у дерева несколько поддеревьев, то имеем:<br><tex>T_2 = 1 + \Sigma_{u \in children(root)}T_2(u) \leqslant 1 + \Sigma_{u \in children(root)}(T_0(u) - 1)</tex> <tex> \leqslant -1 + \Sigma_{u \in children}T_0(u) \leqslant -1 + T_0 = T_0 - 1</tex>. | ||
| + | Заметим, что для леса деревьев лемма также справедлива. | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Лемма | ||
| + | |about=2 | ||
| + | |statement=После применения операций <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> к лесу, математическое ожидание количества вершин в нём не превосходит <tex>\frac{7}{8}</tex> от их исходного числа. | ||
| + | |proof=Математическое ожидание количества удаленных вершин <tex>\mathrm{deleted} = T_0 + \frac{T_1}{8}</tex> (так как все листья будут удалены после операции <tex>\mathrm{Rake}</tex>, а каждая вершина, у которой ровно один сын, будет удалена с вероятностью <tex>1</tex> после операции <tex>\mathrm{Compress}</tex>). Из предыдущей леммы получаем:<br> | ||
| + | <tex>\mathrm{deleted} = \frac{1}{2} (T_0 + T_2) + \frac{1}{8} T_1 \geqslant \frac{1}{8} (T_0 + T_1 + T_2)</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |statement=Математическое ожидание количества операций <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex>, которые будут выполнены до полного сжатия дерева, равно <tex>O(\log{n})</tex>, где <tex>n</tex> {{---}} общее количество вершин. | ||
| + | |proof=Из леммы 2 известно, что после каждой итерации применения операций <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> число вершин в среднем уменьшается в константное число раз. Значит, количество итераций в среднем ограничено <tex>O(\log{n})</tex>. | ||
| + | }} | ||
| + | |||
| + | ==Построение== | ||
| + | |||
| + | ==Возможность параллельного построения== | ||
| + | Операции <tex>\mathrm{Rake}</tex> и <tex>\mathrm{Compress}</tex> можно выполнять параллельно для всех вершин. Если предположить, что множество детей можно пересчитывать за <tex>O(1)</tex>, то Rake-Compress дерево можно построить за <tex>O(\log{n})</tex> в модели PRAM в случае наличия <tex>\Omega(n)</tex> процессоров. | ||
| + | |||
| + | ==Пример выполнения операций== | ||
| + | |||
| + | ==Применения== | ||
| + | * Задача [[Остовные_деревья:_определения,_лемма_о_безопасном_ребре|MST]] online: дан граф <tex>G</tex> из <tex>n</tex> вершин, в который добавляются новые рёбра. Необходимо поддерживать минимальный остовный лес для данного графа, | ||
| + | * Задача о максимальном потоке: в помощью динамических деревьев можно улучшить ассимптотику [[Схема_алгоритма_Диница|алгоритма Диница]] с <tex>O(V^2 E)</tex> до <tex>O(VE \log{V})</tex>. | ||
==См. также== | ==См. также== | ||
| Строка 23: | Строка 55: | ||
* [https://en.wikipedia.org/wiki/Parallel_Tree_Contraction Wikipedia {{---}} Parallel Tree Contraction] | * [https://en.wikipedia.org/wiki/Parallel_Tree_Contraction Wikipedia {{---}} Parallel Tree Contraction] | ||
* [https://github.com/BorysMinaiev/bachelor/blob/master/thesis_v2.pdf Б. Ю. Минаев {{---}} Реализация динамических Rake-Compress деревьев в случае отсутствия ограничения на степени вершин] | * [https://github.com/BorysMinaiev/bachelor/blob/master/thesis_v2.pdf Б. Ю. Минаев {{---}} Реализация динамических Rake-Compress деревьев в случае отсутствия ограничения на степени вершин] | ||
| − | * G. | + | * G. L. Miller, J. H. Reif {{---}} Parallel Tree Contraction |
| − | + | * R. Werneck {{---}} Design and Analysis of Data Structures for Dynamic Trees | |
| + | |||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
Версия 22:47, 18 апреля 2016
Задача, которая решается с помощью динамических деревьев (англ. dynamic tree), формулируется следующим образом. Необходимо поддерживать лес деревьев и выполнять на нем следующие операции:
- добавить ребро . Вершина должна быть корнем некоторого дерева. Вершины и должны находиться в разных деревьях,
- удалить ребро . Ребро должно присутствовать в графе,
- некоторый запрос относительно структуры дерева.
Примером последней операции может быть запрос "достижима ли вершина из ?", "сколько ребер на кратчайшем пути из в ?" или "какова сумма номеров вершин, которые находятся в поддереве вершины ?". Можно легко реализовать структуру данных, которая будет выполнять данные операции за время , где — количество вершин в графе. Динамические деревья нужны для того, чтобы обрабатывать запросы более эффективно. В частности, все предложенные операции возможно выполнять за время .
Содержание
Описание
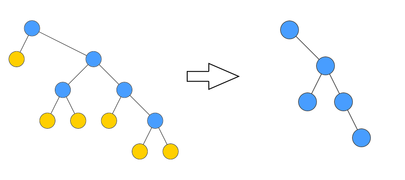
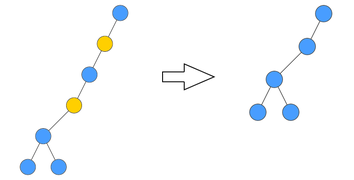
Rake-Compress Tree — структура данных, которая хранит лес деревьев и поддерживает следующие операции:
- — все листья дерева сжимаются к своим родителям,
- — выбирается и объединяется некоторое множество несмежных друг с другом вершин, имеющих ровно одного сына.
Входными данными для алгоритма Rake-Compress является лес корневых деревьев. К нему поочередно применяются операции и до тех пор, пока существует хотя бы одна живая вершина.
Во время каждой из этих операций выбирается некоторое множество попарно несмежных вершин, которое сжимается к своим родителям. После каждой операции лес сохраняется в специальном виде, что в дальнейшем дает возможность отвечать на запросы о структуре леса.
Современная реализация Rake-Compress деревьев была предложена Р. А. Тарьяном и Р. Ф. Вернеком.
Рассмотрим, как изменяется количество вершин в дереве после применения к нему операций и . Разобьём все вершины дерева на три группы: входящая степень которых равна нулю, одному и больше одного. Обозначим их количество за и соответственно.
| Лемма (1): |
. |
| Доказательство: |
|
Докажем по индукции по высоте дерева. |
| Лемма (2): |
После применения операций и к лесу, математическое ожидание количества вершин в нём не превосходит от их исходного числа. |
| Доказательство: |
|
Математическое ожидание количества удаленных вершин (так как все листья будут удалены после операции , а каждая вершина, у которой ровно один сын, будет удалена с вероятностью после операции ). Из предыдущей леммы получаем: |
| Теорема: |
Математическое ожидание количества операций и , которые будут выполнены до полного сжатия дерева, равно , где — общее количество вершин. |
| Доказательство: |
| Из леммы 2 известно, что после каждой итерации применения операций и число вершин в среднем уменьшается в константное число раз. Значит, количество итераций в среднем ограничено . |
Построение
Возможность параллельного построения
Операции и можно выполнять параллельно для всех вершин. Если предположить, что множество детей можно пересчитывать за , то Rake-Compress дерево можно построить за в модели PRAM в случае наличия процессоров.
Пример выполнения операций
Применения
- Задача MST online: дан граф из вершин, в который добавляются новые рёбра. Необходимо поддерживать минимальный остовный лес для данного графа,
- Задача о максимальном потоке: в помощью динамических деревьев можно улучшить ассимптотику алгоритма Диница с до .
См. также
Источники информации
- Wikipedia — Parallel Tree Contraction
- Б. Ю. Минаев — Реализация динамических Rake-Compress деревьев в случае отсутствия ограничения на степени вершин
- G. L. Miller, J. H. Reif — Parallel Tree Contraction
- R. Werneck — Design and Analysis of Data Structures for Dynamic Trees