Деревья Эйлерова обхода — различия между версиями
Sokolova (обсуждение | вклад) (→Balanced Trees) |
Sokolova (обсуждение | вклад) (→Balanced Trees) |
||
| Строка 100: | Строка 100: | ||
===Balanced Trees=== | ===Balanced Trees=== | ||
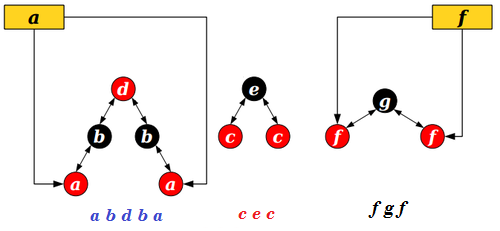
| + | [[Файл:Balanced tree.png |center|Пример ]] | ||
| + | Представим последовательность вершин эйлерова обхода в виде сбалансированного двоичного дерева. Будем использовать красно-черное дерево. | ||
| + | Объединение и разделение красно-черных деревьев выполняется за O(log n). | ||
| − | + | Для каждой вершины храним указатели на её первое и последнее вхождение в последовательность. Значит, имеем доступ к ним за <tex>О(1)</tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Запрос о принадлежности вершин к одной компоненте связности выполняется за O(log n) проверкой лежат ли эти вершины в одном дереве. | |
[[Файл:Balanced tree1.png |center|Пример ]] | [[Файл:Balanced tree1.png |center|Пример ]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Похожие структуры== | ==Похожие структуры== | ||
Про link-cut trees | Про link-cut trees | ||
Версия 17:12, 4 декабря 2016
Содержание
Введение
Для решения задачи о динамической связности (англ.dynamic connectivity problem) требуется выполнение следующих операций:
- — добавить ребро (u, w) (при условии, что вершины u w принадлежат разным деревьям),
- — разрезать ребро (u, w) (при условии, что ребро (u, w) принадлежит дереву),
- — определить принадлежат ли вершины u и w одной компоненте связности.
Дерево эйлерова обхода (англ.Euler tour tree) — способ представления динамического дерева, позволяющий выполнять указанные операции за .
Представление деревьев в виде эйлерова графа
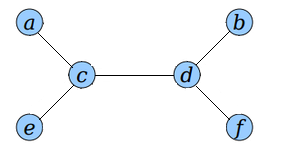
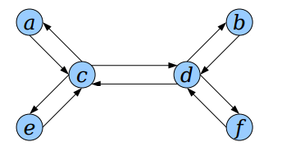
Для представления дерева в виде эйлерового графа заменим каждое ребро дерева на два ребра и .
Получившийся ориентированный граф будет эйлеровым согласно критерию.
Свойство эйлерова обхода
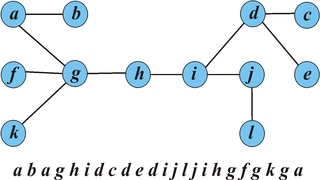
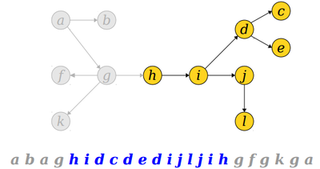
Представим дерево в виде последовательности вершин, посещеннных в порядке эйлерова обхода с корнем в вершине .
При этом последовательность вершин между первым и последним вхождением вершины дает эйлеров обход поддерева с корнем .
Операции
Изменение корня дерева (переподвешивание)
Дано дерево с корнем в вершине . Требуется переподвесить его к вершине .
Для переподвешивания (англ. rerooting) необходимо:
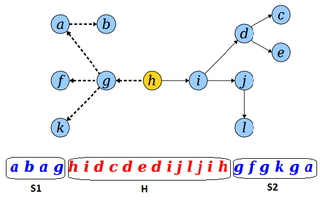
- Разбить эйлеров обход на три части , , и , где состоит из вершин между первым и последним вхождением нового корня .
- Удалить первую вершину в .
- Соединить в следующем порядке: , , .
- Добавить в конец последовательности.
В результате получим:
Добавление ребра
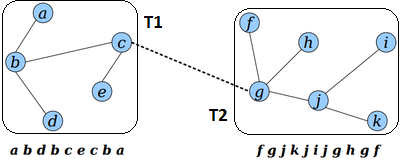
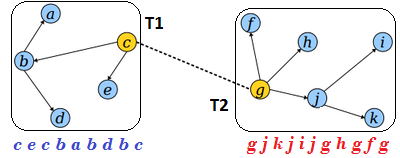
Для связывания деревьев и , где , а добавлением ребра необходимо:
- Переподвесить дерево к вершине .
- Переподвесить дерево к вершине .
- Соединить получившиеся эйлеровы обходы.
- Добавить в конец последовательности.
В результате получим:
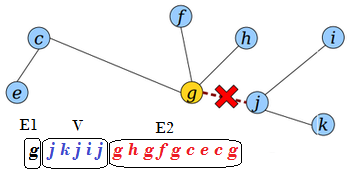
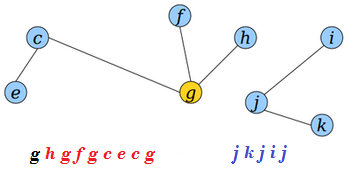
Разрезание ребра
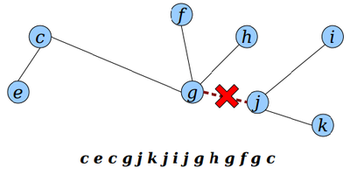
Для разбиения дерева на два поддерева путем разрезания ребра (если оно существует) необходимо:
- Переподвесить дерево к вершине .
- Разделить дерево на части , где отрезок между первым и последним вхождением вершины .
- Эйлеров обход первого поддерева образуется соединением и , с удалением повторного в месте их соединения.
- Эйлеров обход второго поддерева образует .
В результате получим:
Реализация структуры
| Задача: |
| Определить структуру данных для хранения эйлеровых обходов деревьев для наиболее эффективного выполнения указанных операций. |
При представлении деревьев в виде их эйлерова обхода выполнение каждой операции и сводится к соединений и разбиений отрезков в последовательности вершин эйлерова обхода.
Рассмотрим следующие структуры данных для определения времени выполнения разбиения и соединения последовательностей, а также определение принадлежности вершин одной компоненте связности.
Связные списки
Каждое разбиение и соединение последовательностей требует .
Для каждой вершины будем хранить указатели на первое и последнее вхождение вершины в последовательность. Тогда возможно определять первое и последнее вхождение вершины за .
Однако,используя двусвязные списки определение принадлежности вершин одной компоненте связности занимает в худшем случае.
Balanced Trees
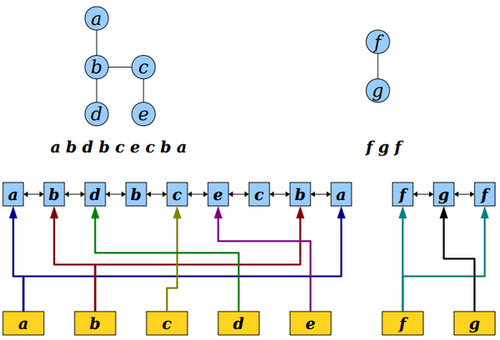
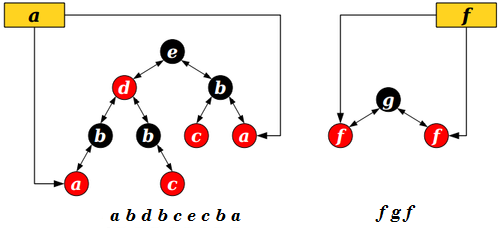
Представим последовательность вершин эйлерова обхода в виде сбалансированного двоичного дерева. Будем использовать красно-черное дерево.
Объединение и разделение красно-черных деревьев выполняется за O(log n).
Для каждой вершины храним указатели на её первое и последнее вхождение в последовательность. Значит, имеем доступ к ним за .
Запрос о принадлежности вершин к одной компоненте связности выполняется за O(log n) проверкой лежат ли эти вершины в одном дереве.
Похожие структуры
Про link-cut trees