Пересечение полуплоскостей, связь с выпуклыми оболочками — различия между версиями
(→Связь с двойственным пространством) |
(→Связь пересечения полуплоскостей с выпуклой оболочкой) |
||
| Строка 76: | Строка 76: | ||
{{Лемма | {{Лемма | ||
|id=1 | |id=1 | ||
| − | |statement= Пересечение полуплоскостей может быть получено построением выпуклой оболочки в [[двойственное пространство|двойственном прострастве]] для множества точек, являющихся дуальным преобразованием | + | |statement= Пересечение полуплоскостей может быть получено построением выпуклой оболочки в [[двойственное пространство|двойственном прострастве]] для множества точек, являющихся дуальным преобразованием исходных полуплоскостей |
|proof= | |proof= | ||
'''Важно:''' Покажем конструктивный алгоритм для множестве полуплоскостей, не содержащих вертикальный полуплоскости. После леммы приведены два рассуждения, позволяющие снять данное ограничение. | '''Важно:''' Покажем конструктивный алгоритм для множестве полуплоскостей, не содержащих вертикальный полуплоскости. После леммы приведены два рассуждения, позволяющие снять данное ограничение. | ||
| − | Рассмотрим планарный случай и предположим, что | + | Рассмотрим планарный случай и предположим, что вертикальные прямые отсутствуют (в конце приведем два способа решения данной проблемы). |
| + | Пусть у нас есть множество ориентированных прямых, каждая из которых задает полуплоскость(направление вектора нормали задаёт нужную полуплоскость). | ||
| + | Тогда каждую плоскость мы можем превратить в точку в двойственном пространстве: <tex> P(p_x, p_y) => P^\star (p_x x - p_y)</tex> | ||
| + | |||
| + | Далее воспользуемся основными свойствами дуальной трансформации (см. доказательтсво в конспекте о [[двойственное пространство|двойственном прострастве]]): | ||
| + | #<tex>p</tex> <tex>\in</tex> <tex>l</tex> <tex>\Leftrightarrow</tex> <tex>l^\star</tex> <tex>\in</tex> <tex>p^\star</tex>, где <tex>p</tex> - точка в исходном пространстве, <tex>l</tex> - прямая в исходном пространстве, <tex>l^\star</tex>, <tex>p^\star</tex> - их дуальное отображение. | ||
| + | #<tex>p</tex> лежит "над" <tex>l</tex> <tex>\Leftrightarrow</tex> <tex>l^\star</tex> лежит "над" <tex>p^\star</tex> | ||
}} | }} | ||
| Строка 87: | Строка 93: | ||
Утверждение выше может быть выведено из '''[[двойственное пространство|двойственного простраства]].''' | Утверждение выше может быть выведено из '''[[двойственное пространство|двойственного простраства]].''' | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Источники == | == Источники == | ||
Версия 20:14, 11 декабря 2016
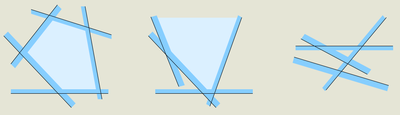
Задача: есть конечное множество полуплоскостей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскость выпукла)
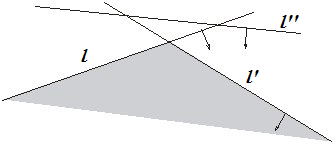
Пусть полуплоскости заданы уравнениями прямых и ориентацией, с какой стороны от прямой лежит полуплоскость.
Сначала рассмотрим все полуплоскости, которые "смотрят", то есть ориентированны, вниз. Аналогично можно рассмотреть все полуплоскости, которые ориентированны вверх.
| Лемма: |
| Доказательство: |
|
Для проверки предиката нужно определить знак выражения , где — точка пересечения прямых и . Эта точка находится из уравнения . Решением будет . Подставим это решение в и домножим на определитель. |
Таким образом, если представить прямую как точку с однородными координатами , то этот предикат — всего лишь поворот, а проверка предиката — проверка очередной точки в обходе Грэхема для нахождения выпуклой оболочки.
Алгоритм:
- Отсортировать все полуплоскости по углу наклона;
- Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем);
- Запустить обход Грэхема для полуплоскостей, смотрящих вверх;
- Пересечь две цепочки.
От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная — когда обе цепочки не пусты и пересекаются.
Связь пересечения полуплоскостей с выпуклой оболочкой
| Лемма: |
Пересечение полуплоскостей может быть получено построением выпуклой оболочки в двойственном прострастве для множества точек, являющихся дуальным преобразованием исходных полуплоскостей |
| Доказательство: |
|
Важно: Покажем конструктивный алгоритм для множестве полуплоскостей, не содержащих вертикальный полуплоскости. После леммы приведены два рассуждения, позволяющие снять данное ограничение. Рассмотрим планарный случай и предположим, что вертикальные прямые отсутствуют (в конце приведем два способа решения данной проблемы). Пусть у нас есть множество ориентированных прямых, каждая из которых задает полуплоскость(направление вектора нормали задаёт нужную полуплоскость). Тогда каждую плоскость мы можем превратить в точку в двойственном пространстве: Далее воспользуемся основными свойствами дуальной трансформации (см. доказательтсво в конспекте о двойственном прострастве):
|
Утверждение выше может быть выведено из двойственного простраства.