AA-дерево — различия между версиями
| Строка 87: | Строка 87: | ||
== Операции == | == Операции == | ||
=== Вставка элемента === | === Вставка элемента === | ||
| − | Рекурсивная реализация. Спускаемся от корня вниз по дереву, сравнивая ключи; вставляем новую вершину; | + | Рекурсивная реализация. Спускаемся от корня вниз по дереву, сравнивая ключи; вставляем новую вершину; выходя из рекурсии и выполняем балансировку: skew и split для каждой вершины. |
'''function''' insert '''is''' | '''function''' insert '''is''' | ||
| Строка 180: | Строка 180: | ||
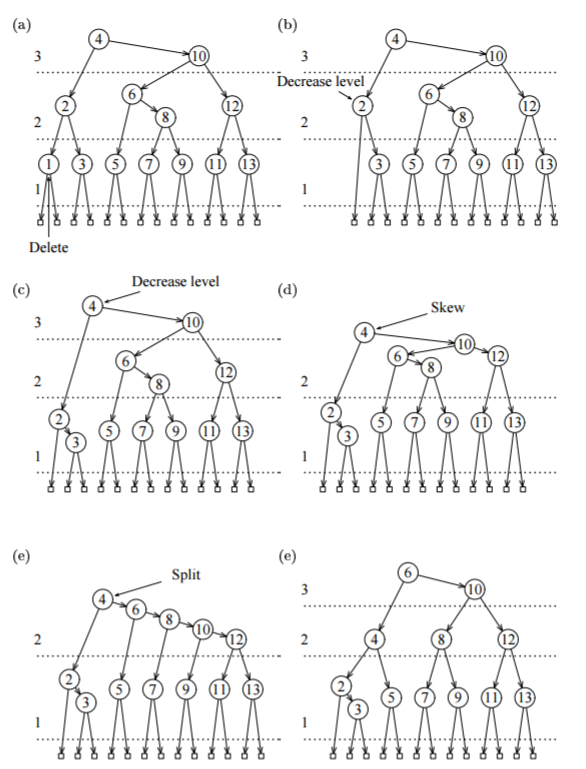
[[Файл: Exdelete.png]] | [[Файл: Exdelete.png]] | ||
| + | |||
| + | == Эффективность == | ||
| + | Скорость работы AA - дерева эквивалентна скорости работы красно-черного дерева. В среднем более простые алгоритмы на AA - дерева выполняются быстрее, но в красно-черном дереве делается меньше поворотов, что уравновешивает асимптотику. | ||
Версия 01:01, 20 декабря 2016
АA-дерево (англ. AA-Tree) — структура данных, представляющая собой сбалансированное двоичное дерево поиска, которое является разновидностью красно-черного дерева с дополнительными ограничениями.
АA-дерево названо по первым буквам имени и фамилии изобретателя, Арне Андерссона, который впервые предложил данную модификацию B-дерева в 1993 году.
| Определение: |
| Уровень вершины (англ. Level) - вертикальная высота соответствующей вершины. Уровень листа равен 1. |
В отличие от красно-черных деревьев, к одной вершине можно присоединить вершину только того же уровня, только одну и только справа (другими словами, красные вершины могут быть добавлены только в качестве правого ребенка).
Содержание
[убрать]Свойства
- Уровень каждого листа равен 1.
- Уровень каждого левого ребенка ровно на один меньше, чем у его родителя.
- Уровень каждого правого ребенка равен или один меньше, чем у его родителя.
- Уровень каждого правого внука строго меньше, чем у его прародителя.
- Каждая вершина с уровнем больше 1 имеет двоих детей.
Для поддержки баланса красно-черного дерева необходимо обрабатывать 7 различных вариантов расположения вершин:
В АА-дереве из-за строгих ограничений необходимо обрабатывать только два вида возможных расположений вершин:
Балансировка
| Определение: |
| Горизонтальное ребро (англ. Horizontal edges) - ребро, соединяющее вершины с одинаковым уровнем. |
В AA - дереве разрешены правые ребра, не идущие подряд, и запрещены все левые горизонтальные ребра.
Эти более жесткие ограничения , аналогичные ограничениям на красно-черных деревьях, приводят к более простой реализации балансировки AA - дерева.
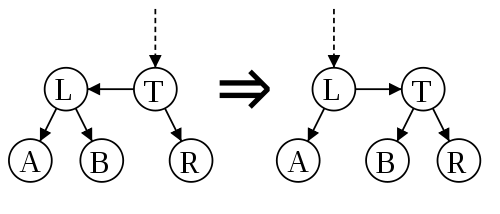
Для балансировки АА-дерева нужны следующие две операции:
- Skew(T) — устранение левого горизонтального ребра.
function skew is
input: T, a node representing an AA tree that needs to be rebalanced.
output: Another node representing the rebalanced AA tree.
if T == NULL then
return NULL
else if left(T) == NULL then
return T
else if level(left(T)) == level(T) then
Swap the pointers of horizontal left links.
L = left(T)
left(T) := right(L)
right(L) := T
return L
else
return T
end if
end function
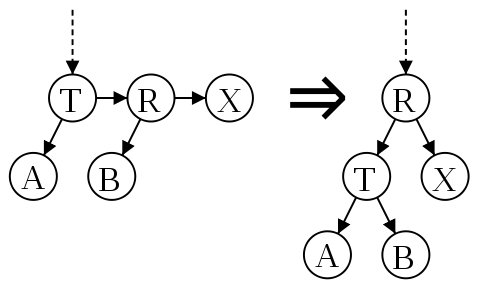
- Split(T) — устранение двух последовательных правых горизонтальных ребер.
function split is
input: T, a node representing an AA tree that needs to be rebalanced.
output: Another node representing the rebalanced AA tree.
if nil(T) then
return Nil
else if nil(right(T)) or nil(right(right(T))) then
return T
else if level(T) == level(right(right(T))) then
We have two horizontal right links. Take the middle node, elevate it, and return it.
R = right(T)
right(T) := left(R)
left(R) := T
level(R) := level(R) + 1
return R
else
return T
end if
end function
Операции
Вставка элемента
Рекурсивная реализация. Спускаемся от корня вниз по дереву, сравнивая ключи; вставляем новую вершину; выходя из рекурсии и выполняем балансировку: skew и split для каждой вершины.
function insert is
input: X, the value to be inserted, and T, the root of the tree to insert it into.
output: A balanced version T including X.
Do the normal binary tree insertion procedure. Set the result of the
recursive call to the correct child in case a new node was created or the
root of the subtree changes.
if nil(T) then
Create a new leaf node with X.
return node(X, 1, Nil, Nil)
else if X < value(T) then
left(T) := insert(X, left(T))
else if X > value(T) then
right(T) := insert(X, right(T))
end if
Note that the case of X == value(T) is unspecified. As given, an insert
will have no effect. The implementor may desire different behavior.
Perform skew and then split. The conditionals that determine whether or
not a rotation will occur or not are inside of the procedures, as given
above.
T := skew(T)
T := split(T)
return T
end function
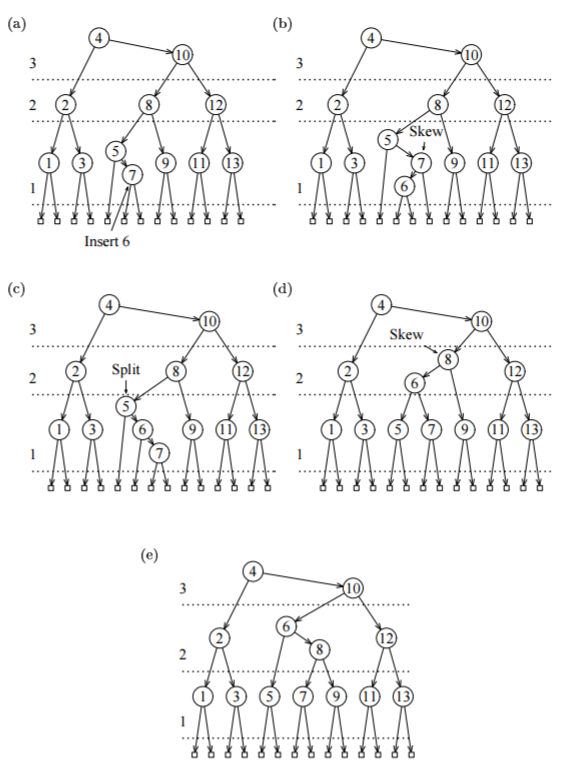
Пример вставки нового элемента (на рис. уровни разделены горизонтальными линиями):
Удаление вершины
Рекурсивная реализация. Как и в большинстве сбалансированных бинарных деревьев, удаление внутренней вершины можно заменить на удаление листа, если заменить внутреннюю вершину на ее ближайшего "предшественника" (англ. predecessor) или "преемника" (англ. successor), в зависимости от реализации. "Предшественник" находиться в начале последнего левого ребра, после которого идут все правые ребра. По аналогии, "преемник" может быть найден после одного правого ребра и последовательности левых ребер, пока не будет найден указатель на NULL. В силу свойства всех узлов уровня более чем 1, имеющих двух детей, предшественник или преемник будет на уровне 1, что делает их удаление тривиальным.
Чтобы сохранять баланс дерева необходимо делать skew, split и корректировку уровня для каждой вершины.
function delete is
input: X, the value to delete, and T, the root of the tree from which it should be deleted.
output: T, balanced, without the value X.
if nil(T) then
return T
else if X > value(T) then
right(T) := delete(X, right(T))
else if X < value(T) then
left(T) := delete(X, left(T))
else
If we're a leaf, easy, otherwise reduce to leaf case.
if leaf(T) then
return Nil
else if nil(left(T)) then
L := successor(T)
right(T) := delete(value(L), right(T))
value(T) := value(L)
else
L := predecessor(T)
left(T) := delete(value(L), left(T))
value(T) := value(L)
end if
end if
Rebalance the tree. Decrease the level of all nodes in this level if
necessary, and then skew and split all nodes in the new level.
T := decrease_level(T)
T := skew(T)
right(T) := skew(right(T))
if not nil(right(T))
right(right(T)) := skew(right(right(T)))
end if
T := split(T)
right(T) := split(right(T))
return T
end function
function decrease_level is
input: T, a tree for which we want to remove links that skip levels.
output: T with its level decreased.
should_be = min(level(left(T)), level(right(T))) + 1
if should_be < level(T) then
level(T) := should_be
if should_be < level(right(T)) then
level(right(T)) := should_be
end if
end if
return T
end function
Пример удаления вершины (на рис. уровни разделены горизонтальными линиями):
Эффективность
Скорость работы AA - дерева эквивалентна скорости работы красно-черного дерева. В среднем более простые алгоритмы на AA - дерева выполняются быстрее, но в красно-черном дереве делается меньше поворотов, что уравновешивает асимптотику.