Дерево поиска, наивная реализация

Бинарное дерево поиска из 9 элементов

Бинарное дерево поиска (англ. binary search tree, BST) — структура данных для работы с упорядоченными множествами.

Бинарное дерево поиска обладает следующим свойством: если [math]x[/math] — узел бинарного дерева с ключом [math]k[/math], то все узлы в левом поддереве должны иметь ключи, меньшие [math]k[/math], а в правом поддереве большие [math]k[/math].

Операции в бинарном дереве поиска

Для представления бинарного дерева поиска в памяти будем использовать следующую структуру:

struct Node:
  T key                    // ключ узла
  Node left                // указатель на левого потомка
  Node right               // указатель на правого потомка
  Node parent              // указатель на предка

Обход дерева поиска

Есть три операции обхода узлов дерева, отличающиеся порядком обхода узлов:

• [math]\mathrm{inorderTraversal}[/math] — обход узлов в отсортированном порядке,
• [math]\mathrm{preorderTraversal}[/math] — обход узлов в порядке: вершина, левое поддерево, правое поддерево,
• [math]\mathrm{postorderTraversal}[/math] — обход узлов в порядке: левое поддерево, правое поддерево, вершина.

func inorderTraversal(x : Node):
   if x != null
      inorderTraversal(x.left)
      print x.key
      inorderTraversal(x.right)

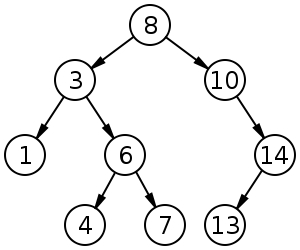
При выполнении данного обхода вершины будут выведены в следующем порядке: 1 3 4 6 7 8 10 13 14.

func preorderTraversal(x : Node)
   if x != null
      print x.key
      preorderTraversal(x.left)
      preorderTraversal(x.right)

При выполнении данного обхода вершины будут выведены в следующем порядке: 8 3 1 6 4 7 10 14 13.

func postorderTraversal(x : Node)
   if x != null
      postorderTraversal(x.left)
      postorderTraversal(x.right)
      print x.key

При выполнении данного обхода вершины будут выведены в следующем порядке: 1 4 7 6 3 13 14 10 8.

Данные алгоритмы выполняют обход за время [math]O(n)[/math], поскольку процедура вызывается ровно два раза для каждого узла дерева.

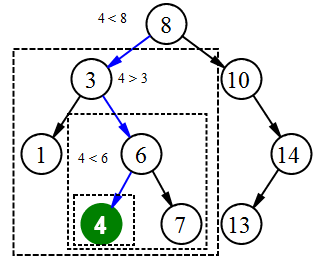
Поиск элемента

Поиск элемента 4

Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей функцией, которая принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы [math]O(h)[/math], где [math]h[/math] — высота дерева.

Node search(x : Node, k : T):
   if x == null or k == x.key
      return x
   if k < x.key
      return search(x.left, k)
   else
      return search(x.right, k)

Поиск минимума и максимума

Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям [math]left[/math] от корня дерева, пока не встретится значение [math]null[/math]. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.

Node minimum(x : Node):
  if x.left == null
     return x
  return minimum(x.left)

Node maximum(x : Node):
  if x.right == null
     return x
  return maximum(x.right)

Данные функции принимают корень поддерева, и возвращают минимальный (максимальный) элемент в поддереве. Обе процедуры выполняются за время [math]O(h)[/math].

Поиск следующего и предыдущего элемента

Реализация с использованием информации о родителе

Если у узла есть правое поддерево, то следующий за ним элемент будет минимальным элементом в этом поддереве. Если у него нет правого поддерева, то нужно следовать вверх, пока не встретим узел, который является левым дочерним узлом своего родителя. Поиск предыдущего выполнятся аналогично. Если у узла есть левое поддерево, то следующий за ним элемент будет максимальным элементом в этом поддереве. Если у него нет левого поддерева, то нужно следовать вверх, пока не встретим узел, который является правым дочерним узлом своего родителя.

Node next(x : Node):
   if x.right != null
      return minimum(x.right)
   y = x.parent
   while y != null and x == y.right
      x = y
      y = y.parent
   return y

Node prev(x : Node):
   if x.left != null
      return maximum(x.left)
   y = x.parent
   while y != null and x == y.left
      x = y
      y = y.parent
   return y

Обе операции выполняются за время [math]O(h)[/math].

Реализация без использования информации о родителе

Рассмотрим поиск следующего элемента для некоторого ключа [math]x[/math]. Поиск будем начинать с корня дерева, храня текущий узел [math]current[/math] и узел [math]successor[/math], последний посещенный узел, ключ которого больше [math]x[/math].
Спускаемся вниз по дереву, как в алгоритме поиска узла. Рассмотрим ключ текущего узла [math]current[/math]. Если [math]current.key \leqslant x[/math], значит следующий за [math]x[/math] узел находится в правом поддереве (в левом поддереве все ключи меньше [math]current.key[/math]). Если же [math]x \lt current.key[/math], то [math]x \lt next(x) \leqslant current.key[/math], поэтому [math]current[/math] может быть следующим для ключа [math]x[/math], либо следующий узел содержится в левом поддереве [math]current[/math]. Перейдем к нужному поддереву и повторим те же самые действия.
Аналогично реализуется операция поиска предыдущего элемента.

Node next(x : T):
   Node current = root, successor = null                // root — корень дерева
   while current != null
      if current.key > x
         successor = current
         current = current.left
      else
         current = current.right
   return successor

Вставка

Операция вставки работает аналогично поиску элемента, только при обнаружении у элемента отсутствия ребенка нужно подвесить на него вставляемый элемент.

Реализация с использованием информации о родителе

func insert(x : Node, z : Node):            // x — корень поддерева, z — вставляемый элемент
   while x != null
     if z.key > x.key
        if x.right != null
           x = x.right
        else
           z.parent = x
           x.right = z
           break
     else if z.key < x.key
        if x.left != null
           x = x.left
        else
           z.parent = x
           x.left = z
           break

Реализация без использования информации о родителе

Node insert(x : Node, z : T):               // x — корень поддерева, z — вставляемый ключ
   if x == null 
      return Node(z)                        // подвесим Node с key = z
   else if z < x.key
      x.left = insert(x.left, z)
   else if z > x.key
      x.right = insert(x.right, z)
   return x

Время работы алгоритма для обеих реализаций — [math]O(h)[/math].

Удаление

Нерекурсивная реализация

Для удаления узла из бинарного дерева поиска нужно рассмотреть три возможные ситуации. Если у узла нет дочерних узлов, то у его родителя нужно просто заменить указатель на [math]null[/math]. Если у узла есть только один дочерний узел, то нужно создать новую связь между родителем удаляемого узла и его дочерним узлом. Наконец, если у узла два дочерних узла, то нужно найти следующий за ним элемент (у этого элемента не будет левого потомка), его правого потомка подвесить на место найденного элемента, а удаляемый узел заменить найденным узлом. Таким образом, свойство бинарного дерева поиска не будет нарушено. Данная реализация удаления не увеличивает высоту дерева. Время работы алгоритма — [math]O(h)[/math].

Случай	Иллюстрация
Удаление листа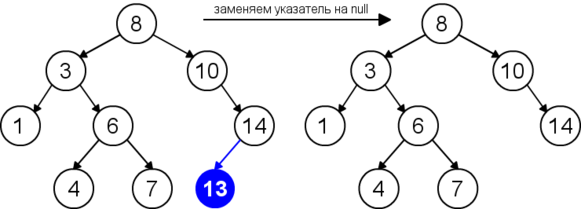
Удаление узла с одним дочерним узлом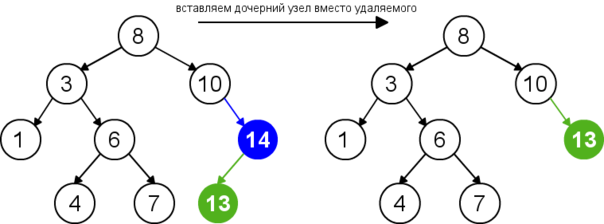
Удаление узла с двумя дочерними узлами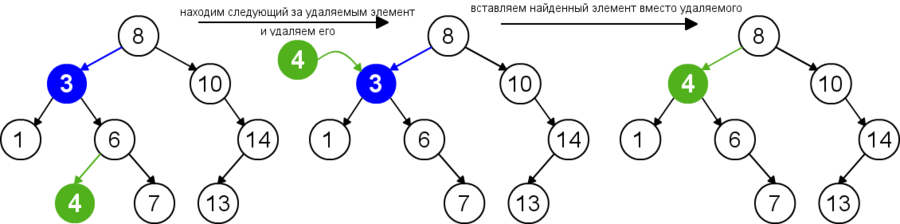

func delete(t : Node, v : Node):                 // [math]t[/math] — дерево, [math]v[/math] — удаляемый элемент
   p = v.parent                                  // предок удаляемого элемента
   if v.left == null and v.right == null         // первый случай: удаляемый элемент - лист
     if p.left == v
       p.left = null
     if p.right == v
       p.right = null
   else if v.left == null or v.right == null     // второй случай: удаляемый элемент имеет одного потомка
       if v.left == null                 
           if p.left == v
             p.left = v.right
           else
             p.right = v.right
           v.right.parent = p 
       else
           if p.left == v
               p.left = v.left
           else
               p.right = v.left
           v.left.parent = p
   else                                          // третий случай: удаляемый элемент имеет двух потомков
     successor = next(v, t)                   
     v.key = successor.key
     if successor.parent.left == successor
       successor.parent.left = successor.right
       if successor.right != null
         successor.right.parent = successor.parent
     else
       successor.parent.right = successor.right
       if successor.right != null
         successor.right.parent = successor.parent

Рекурсивная реализация

При рекурсивном удалении узла из бинарного дерева нужно рассмотреть три случая: удаляемый элемент находится в левом поддереве текущего поддерева, удаляемый элемент находится в правом поддереве или удаляемый элемент находится в корне. В двух первых случаях нужно рекурсивно удалить элемент из нужного поддерева. Если удаляемый элемент находится в корне текущего поддерева и имеет два дочерних узла, то нужно заменить его минимальным элементом из правого поддерева и рекурсивно удалить минимальный элемент из правого поддерева. Иначе, если удаляемый элемент имеет один дочерний узел, нужно заменить его потомком. Время работы алгоритма — [math]O(h)[/math]. Рекурсивная функция, возвращающая дерево с удаленным элементом [math]z[/math]:

Node delete(root : Node, z : T):               // корень поддерева, удаляемый ключ
  if root == null
    return root
  if z < root.key
    root.left = delete(root.left, z)
  else if z > root.key
    root.right = delete(root.right, z)
  else if root.left != null and root.right != null
    root.key = minimum(root.right).key
    root.right = delete(root.right, root.right.key)
  else
    if root.left != null
      root = root.left
    else
      root = root.right
  return root

Задачи о деревьях поиска и произвольных двоичных деревьях

Проверка того, что заданное дерево является деревом поиска

Задача:

Определить, является ли заданное двоичное дерево деревом поиска.

Для того чтобы решить эту задачу, применим обход в глубину. Начнём путь от корня и будем рассматривать для каждой вершины её детей. Если ребёнок не нарушает условия дерева поиска, спускаемся на следующий уровень. Если же нашлась вершина, стоящая не на своём месте, то этого достаточно, чтобы сказать, что заданное дерево не является деревом поиска, и вернуть значение [math]\mathrm{false}[/math]. Если мы дойдём до листьев и не найдём противоречащих условию вершин, возвращаем значение [math]\mathrm{true}[/math].

Псевдокод

bool check(v : Node, min: integer, max: integer):       //min и max - минимально и максимально допустимые значения в вершинах поддерева.
  if v.left != null
    if v.left.key > v.key or v.left.key < min
      return false
    else check(v.left, min, v.key)
    if v.right.key < v.key or v.right.key > max
      return false
    else check(v.right, v.key, max)
  return true

Поиск максимального поддерева, являющегося BST, в заданном двоичном дереве

Задача:

Найти в данном дереве максимальное из поддеревьев поиска.

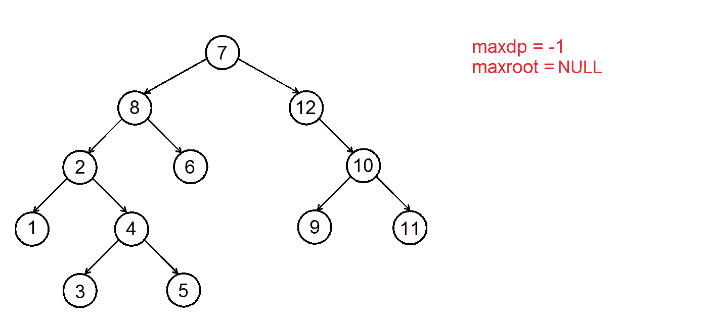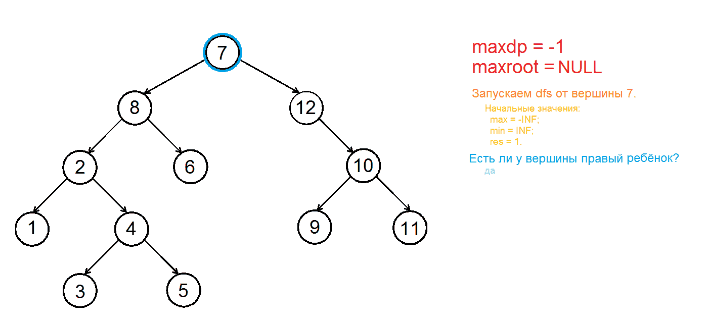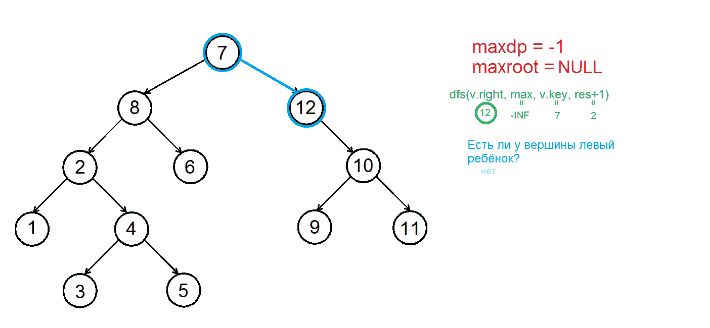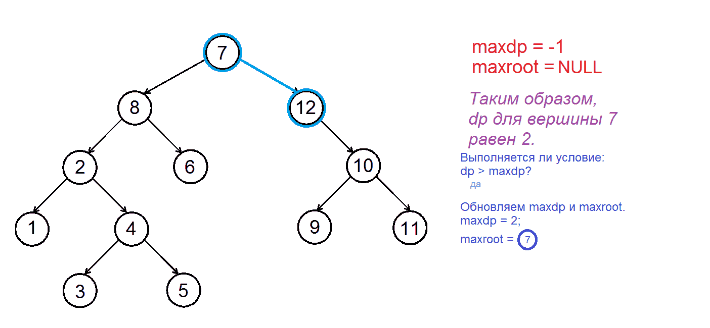
В переменную [math]maxdp[/math], изначально равную [math]-1[/math], запишем число вершин максимального поддерева поиска. Будем также вместе с [math]maxdp[/math] обновлять [math]maxroot[/math], где будет храниться корень такого поддерева. Чтобы найти [math]maxdp[/math], обойдём вершины и для каждой из них с помощью процедуры [math]dfs[/math], на вход которой подаются сама вершина, максимально и минимально возможные элементы поддерева и количество вершин, посчитаем число элементов, принадлежащих максимальному дереву поиска, для которого данная вершина является корнем. Если результат после обхода вершины оказался больше значения в переменной [math]maxdp[/math], обновляем [math]maxdp[/math] и [math]maxroot[/math]. Затем переходим к следующей вершине. После того как мы прошлись по всему дереву, посчитали [math]maxdp[/math] и нашли [math]maxroot[/math], запускаем процедуру [math]dfsPrint(maxroot, -INF, INF)[/math] для вывода вершин поддерева поиска. До запуска процедуры [math]dfs[/math] от каждой вершины переменная [math]dp[/math] равна единице.

maxdp = -1
maxroot = null
for u in Tree          		// Здесь Tree – заданное двоичное дерево.
  dp = 1
  dfs(u, -INF, INF, dp)
  if dp > maxdp
    maxdp = dp
    maxroot = u
dfsPrint(maxroot, -INF, INF)

Процедура [math]dfs(v,max,min,res)[/math] позволяет подсчитать максимальное количество вершин двоичного поддерева поиска с вершиной [math]v[/math]. В начале работы этой процедуры [math]max[/math] и [math]min[/math] принимают нейтральные значения ([math]-INF[/math] и [math]INF[/math] соответственно, где [math]INF[/math] - очень большое число), а [math]res[/math] равен [math]1[/math] (одна вершина в дереве уже имеется). Обход осуществляется следующим образом:

1 шаг. Проверяем, есть ли у вершины левый сын. Если его нет, переходим к пункту 2, иначе сравниваем значения в этой вершине и в её левом потомке, а также значение в левом сыне с максимумом в поддереве. Если значение в левом сыне меньше, чем значение в вершине и больше переменной [math]max[/math], то запускаем [math]dfs[/math] из левого сына. Здесь роль v будет разыгрывать [math]v.left[/math], [math]max[/math] приобретёт значение [math]v.key[/math], [math]min[/math] по-прежнему останется [math]min[/math], а [math]res[/math] увеличится на 1. Пояснение: ключи вершин левого поддерева не должны превосходить значения в рассматриваемой вершине, поэтому мы изменяем [math]max[/math]. На [math]min[/math] эта вершина не влияет в случае левого поддерева, поэтому он не изменяется. [math]res[/math] увеличивается на 1, так как в наше поддерево добавилась ещё одна вершина.

2 шаг. Аналогично действуем с правым потомком. Проверяем его наличие. Если он существует, то сравниваем значение в нём с минимумом и с ключом вершины. Если значение правого сына больше минимума в поддереве и меньше значения в вершине, то запускаем от потомка [math]dfs[/math]. Теперь на место [math]v[/math] встаёт [math]v.right[/math], [math]max[/math] остаётся прежним, [math]min[/math] становится ключом в рассматриваемой вершине, а [math]res[/math] снова увеличивается на 1. Для случая с правым поддеревом рассуждения аналогичны.

3 шаг. Возвращаем результат в переменной [math]res[/math], где записано количество вершин поддерева.

Пример выполнения процедуры dfs для вершины с номером 7

Процедура обхода дерева представлена ниже:

procedure dfs(v: Node, max: T, min: T, res: integer)
  if v.left != null
    if v.left.key < v.key and v.left.key > max
      dfs(v.left, v.left.key, min, res+1)
  if v.right != null
    if v.right.key > v.key and v.right.key < min
      dfs(v.left, max, v.left.key, res+1)

Наконец, рассмотрим процедуру [math]dfsPrint[/math], выводящую максимальное дерево поиска. Так как [math]maxdp[/math] уже посчитано, достаточно задать три параметра: корень поддерева и максимальное и минимальное допустимые значения. [math]max[/math] и [math]min[/math] нам понадобятся, чтобы взять только те вершины, которые принадлежат дереву.

procedure dfsPrint(v: Node, max: T, min: T)
  print v.key
  if v.left != null
    if v.left.key < v.key and v.left.key > max
      dfsPrint(v.left, v.left.key, min)
  if v.right != null
    if v.right.key > v.key and v.right.key < min
      dfsPrint(v.left, max, v.left.key)

Восстановление дерева поиска по последовательности ключей

Заметим, что [math]dfsPrint[/math] выводит значения в узлах поддерева следующим образом: сначала идёт до упора влево, затем делает шаг вправо, потом снова влево и так до тех пор, пока не будет выведено [math]maxdp[/math] вершин. Полученная последовательность позволит нам однозначно определить расположение всех узлов поддерева. Происходит это так:

- последовательно подвешиваем левых сыновей, пока не находим номер, нарушающий убывающую последовательность;

- для каждого номера, нарушающего убывающую последовательность, ищем вершину с наибольшим значением, не превосходящим его, среди вершин без правого потомка и к этому элементу подвешиваем вершину с таким номером в качестве правого сына.

Первое число последовательности всегда находится в корне, так как вывод ключей вершин начинался с него.

Разберём алгоритм на примере последовательности для приведённого выше дерева. Она выглядит так: 8 2 1 4 3 5. Сначала в корень записывается 8. Затем его левым сыном становится вершина с номером 2, а её левым сыном - 1. Следующее значение - 4 - уже нарушает убывающую подпоследовательность. Подберём для него вершину, где лежит значение, меньшее его, причём такая вершина максимальна (в противном случае он будет превосходить и прародителя, находясь в его левом поддереве, а это противоречит определению дерева поиска). Это узел с числом 2. Сделаем его правым сыном рассматриваемую вершину. Затем снова дадим левых потомков последней добавленной вершине, опять же, пока не найдём ключ, нарушающий порядок убывания. В нашем случае в дерево дописывается 3. Для следующего значения снова ищем родителя, для которого он станет правым сыном. Это значение равно 4. Добавляем 5 как правого сына для вершины 4. Итак, мы построили дерево.

См. также

• Поисковые структуры данных
• Рандомизированное бинарное дерево поиска
• Красно-черное дерево

Источники информации

• Википедия — Двоичное дерево поиска
• Wikipedia — Binary search tree
• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4